Question

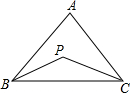
【提出问题】
已知P是∠ABC、∠ACB的角平分线的交点，你能找到∠P、∠A的关系吗？
【分析问题】
在解决这个问题时，小明是这样做的：先找一个例子，如∠A=80°度，计算出∠P=130°，随后他又举了几个例子，并对结论进行了证明，从而找到∠P与∠A的关系：∠P=90°+

1

2

∠A
在解决问题的过程中，小明运用了“由特例得到猜想，证明得出一般结论”的方法，你能用这种方法解决下面的两个问题．
【解决问题】
（1）若点P是∠ABC、∠ACB的三等分线的交点，即∠PBC=

1

3

∠ABC，∠PCB=

1

3

∠ACB，则∠P与∠A的关系为

 

，请证明你的结论．
（2）若P是∠ABC、∠ACB的四等分线交点，∠PBC=

1

4

∠ABC，∠PCB=

1

4

∠ACB，则∠P与∠A的关系为

 

．（直接写出答案，不需证明）
（3）若P是∠ABC、∠ACB的n等分线交点，∠PBC=

1

n

∠ABC，∠PCB=

1

n

∠ACB，则∠P与∠A的关系为

 

．（直接写出答案，不需证明）

Answer 1

考点：三角形内角和定理,三角形的外角性质

专题：探究型

分析：（1）假设∠A=60°，先根据三角形内角和定理求出∠ABC+∠ACB，根据三等分线求出∠PBC+∠PCB，根据三角形的内角和定理得出∠BPC=180°-（∠PBC+∠PCB），代入求出即可；
（2）假设∠A=60°，同（1）可得出结论；
（3）先根据三角形内角和定理求出∠ABC+∠ACB，根据n等分线求出∠PBC+∠PCB，根据三角形的内角和定理得出∠BPC=180°-（∠PBC+∠PCB），代入求出即可．

解答：解：（1）假设∠A=60°，
∵∠A=60°，
∴∠ABC+∠ACB=180°-60°=120°，
∵BP、CP分别是∠ABC、∠ACB的三等分线，
∴∠PBC+∠PCB=

1

3

（180°-60°）=40°，
∴∠P=180°-（∠OBC+∠OCB）=140°，即∠P=

1

3

∠A+

2

3

×180°．
故答案为：∠P=

1

3

∠A+

2

3

×180°；

（2）假设∠A=60°，
∵∠A=60°，
∴∠ABC+∠ACB=180°-60°=120°，
∵BP、CP分别是∠ABC、∠ACB的四等分线，
∴∠PBC+∠PCB=

1

4

（180°-60°）=30°，
∴∠P=180°-（∠OBC+∠OCB）=150°，即∠P=

1

4

∠A+

3

4

×180°．
故答案为：∠P=

1

4

∠A+

3

4

×180°；

（3）∵∠ABC+∠ACB=180°-∠A，BP、CP分别是∠ABC、∠ACB的n等分线，
∴∠PBC+∠PCB=

1

n

（180°-∠A），
∴∠BPC=180°-（∠PBC+∠PCB）
=180°-

1

n

（180°-∠A）
=

n-1

n

•180°+

1

n

∠A．
故答案为：

n-1

n

•180°+

1

n

∠A．

点评：本题考查的是三角形的内角和定理及角平分线定义，解此题的关键是能用∠A表示出∠OBC+∠OCB的度数，题目比较好，求解过程类似．