题目内容
14. 求直线l1:y=5x-5和l2:y=2x+4与x轴、y轴的正半轴所围成的图形PAOB的面积.
求直线l1:y=5x-5和l2:y=2x+4与x轴、y轴的正半轴所围成的图形PAOB的面积.
分析 根据直线的解析式求得直线与坐标轴的交点坐标,然后根据S四边形PAOB=S△PAC-S△BOC求得即可.
解答  解:由直线l1:y=5x-5可知,直线l1与y轴的交点C(0,-5),与x轴的交点B(1,0),由l2:y=2x+4可知直线l2与y轴的交点A(0,4),
解:由直线l1:y=5x-5可知,直线l1与y轴的交点C(0,-5),与x轴的交点B(1,0),由l2:y=2x+4可知直线l2与y轴的交点A(0,4),
∴OA=4,OC=5,OB=1,
∴AC=4+5=9,
解$\left\{\begin{array}{l}{y=5x-5}\\{y=2x+4}\end{array}\right.$得$\left\{\begin{array}{l}{x=3}\\{y=10}\end{array}\right.$,
∴P(3,10),
∴直线l1、l2及与x轴、y轴的正半轴所围成的图形PAOB的面积,即S四边形PAOB=S△PAC-S△BOC=$\frac{1}{2}$×9×3-$\frac{1}{2}$×5×1=11.
点评 本题考查了两条直线相交的问题以及三角形的面积,求得两条直线与坐标轴的交点是解题的关键.

练习册系列答案
相关题目
4.计算(-$\frac{1}{2}$x2y)3+($\frac{1}{4}$x2y)2•(-x2y)的结果为( )
| A. | -$\frac{3}{16}$x6y3 | B. | 0 | C. | -x6y3 | D. | -$\frac{5}{12}$x6y3 |
 如图所示,已知BC=3AB,DA=$\frac{1}{2}$AB,E为DB的中点,若DE=60mm,求BC,DC的长.
如图所示,已知BC=3AB,DA=$\frac{1}{2}$AB,E为DB的中点,若DE=60mm,求BC,DC的长.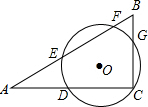 如图,△ABC中,∠ACB=90°,点O为△ABC的角平分线交点,⊙O经过点C,与△ABC的三边交于点D、E、F、G.
如图,△ABC中,∠ACB=90°,点O为△ABC的角平分线交点,⊙O经过点C,与△ABC的三边交于点D、E、F、G.