Question

5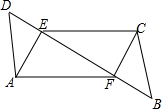．如图，已知AE⊥BD，CF⊥BD，E，F为垂足，AD∥BC，DE=BF，求证：四边形AECF是平行四边形．

Answer 1

分析 根据平行线的性质得到∠B=∠D，由已知条件得到∠AED=∠CFB=90°，AE∥CF，推出△ADE≌△CBF，根据全等三角形的性质得到AE=CF．根据平行四边形的判定定理即可得到结论．

解答 证明：∵AD∥CB，
∴∠B=∠D，
∵AE⊥BD，CF⊥BD，
∴∠AED=∠CFB=90°，AE∥CF，
在△ADE和△CBF中，
$\left\{\begin{array}{l}{∠B=∠D}\\{∠CFB=∠AED}\\{CF=AE}\end{array}\right.$，
∴△ADE≌△CBF，
∴AE=CF．
∵AE∥CF，
∴四边形AECF是平行四边形．

点评 本题考查的是全等三角形及平行四边形的判定定理及性质，是中学阶段的重点内容，需同学们熟练掌握．