题目内容
19.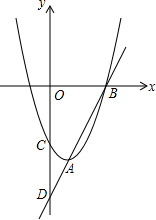 如图,已知直线y=kx-6与抛物线y=ax2+bx+c相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上.直线AB交y轴于点D,抛物线交y轴于点C.
如图,已知直线y=kx-6与抛物线y=ax2+bx+c相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上.直线AB交y轴于点D,抛物线交y轴于点C.(1)求直线AB的解析式;
(2)求抛物线的解析式;
(3)在y轴上是否存在点Q,使△ABQ为直角三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.
分析 (1)把点A坐标代入y=kx-6,根据待定系数法即可求得直线AB的解析式;
(2)根据直线AB的解析式求出点B的坐标,点A是抛物线的顶点,那么可以将抛物线的解析式设为顶点式,再代入点B的坐标,依据待定系数法即可求解;
(3)分别以A、B、Q为直角顶点,分类进行讨论.找出相关的相似三角形,依据对应线段成比例进行求解即可.
解答 解:(1)把A(1,-4)代入y=kx-6,得k=2,
∴直线AB的解析式为y=2x-6,
(2)∵抛物线的顶点为A(1,-4),
∴设此抛物线的解析式为y=a(x-1)2-4,
∵点B在直线y=2x-6上,且横坐标为0,
∴点B的坐标为(3,0),
又∵点B在抛物线y=a(x-1)2-4上,
∴a(3-1)2-4=0,解之得a=1,
∴此抛物线的解析式为y=(x-1)2-4,即y=x2-2x-3;
(3)在y轴上存在点Q,使△ABQ为直角三角形.理由如下:
作AE⊥y轴,垂足为点E.
又∵点D是直线y=2x-6与y轴的交点,点C是抛物线y=x2-2x-3与y轴的交点
∴E(0,-4),D(0,-6),C(0,-3)
∴OD=6,OE=4,AE=1,ED=2,OC=3,OB=3,BD=$3\sqrt{5}$,AD=$\sqrt{5}$
①如图,当∠Q1AB=90°时,△DAQ1∽△DOB,
∴$\frac{AD}{OD}$=$\frac{D{Q}_{1}}{DB}$,即$\frac{\sqrt{5}}{6}$=$\frac{D{Q}_{1}}{3\sqrt{5}}$,
∴DQ1=$\frac{5}{2}$,
∴OQ1=6-$\frac{5}{2}$=$\frac{7}{2}$,即Q1(0,-$\frac{7}{2}$);
②如图,当∠Q2BA=90°时,△BOQ2∽△DOB,
∴$\frac{OB}{OD}$=$\frac{O{Q}_{2}}{OB}$,即$\frac{3}{6}$=$\frac{O{Q}_{2}}{3}$,
∴OQ2=$\frac{3}{2}$,即Q2(0,$\frac{3}{2}$);
③如图,当∠AQ3B=90°时,则△BOQ3∽△Q3EA,
∴$\frac{OB}{E{Q}_{3}}$=$\frac{O{Q}_{3}}{AE}$,即$\frac{3}{4-O{Q}_{3}}$=$\frac{O{Q}_{3}}{1}$,
∴OQ32-4OQ3+3=0,
∴OQ3=1或3,
即Q3(0,-1),Q4(0,-3).
综上,Q点坐标为(0,-$\frac{7}{2}$)或(0,$\frac{3}{2}$)或(0,-1)或(0,-3).
点评 本题主要考查了利用待定系数法求函数解析式的方法、直角三角形的判定、相似三角形应用等重点知识.(3)题较为复杂,需要考虑的情况也较多,因此要分类进行讨论.

 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案 如图所示,∠CAB的外角等于120°,∠B等于40°,则∠C的度数是( )
如图所示,∠CAB的外角等于120°,∠B等于40°,则∠C的度数是( )| A. | 60° | B. | 70° | C. | 80° | D. | 90° |
| A. | 明天下雨的概率大 | |
| B. | 任意抛掷两颗完全相同的均匀的正四面体骰子,其点数之和为11的概率为零 | |
| C. | 随机说出3个正整数,以这三个数为边长一定能围成一个三角形 | |
| D. | 一副扑克牌,去掉大小王,从中任抽一张,恰好抽到的牌是10的概率为$\frac{1}{13}$ |
 已知,如图,在四边形ABCD中,AB=AD,∠ABC=∠ADC,求证:AC平分∠BAD.
已知,如图,在四边形ABCD中,AB=AD,∠ABC=∠ADC,求证:AC平分∠BAD.