题目内容
10.某中学为了绿化校园,计划购买A、B两种树,经过市场调查,A树的单价比B树少20元,购买4棵A树和购买3棵B树的费用相等.(1)求两种树的单价各是多少?
(2)根据学校的实际情况,需购买两种树共150棵,总费用不超过10840元,且购买B树的棵数不少于A树的1.5倍.请你算算,该校本次购买这两种树共有哪几种方案.
分析 (1)设A树的单价是x元,则B树的单价为(x+20)元,根据购买4棵A树和购买3棵B树的费用相等可列方程求解.
(2)设购买A树m棵,则购买B树(150-m)棵,根据总费用不超过10840元,且购买B树的棵数不少于A树的1.5倍,可列不等式组求解.
解答 解:(1)设A树的单价是x元,则B树的单价为(x+20)元,根据题意得
4x=3(x+20),
解得x=60,
则x+20=80.
答:A树的单价是60元,B树的单价为80元;
(2)设购买A树m棵,则购买B树(150-m)棵,根据题意得
$\left\{\begin{array}{l}{60m+80(150-m)≤10840}\\{150-m≥1.5m}\end{array}\right.$,
解得58≤m≤60,
∵m为整数,
∴m为58或59或60.
答:该校本次购买这两种树共有3种方案:①购买A树58棵,购买B树92棵;②购买A树59棵,购买B树91棵;③购买A树60棵,购买B树90棵.
点评 本题考查一元一次方程的应用,一元一次不等式组的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的关系列出方程或不等式组,再求解.

练习册系列答案
相关题目
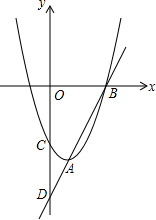 如图,已知直线y=kx-6与抛物线y=ax2+bx+c相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上.直线AB交y轴于点D,抛物线交y轴于点C.
如图,已知直线y=kx-6与抛物线y=ax2+bx+c相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上.直线AB交y轴于点D,抛物线交y轴于点C.