题目内容
在一个不透明的口袋里装有四个分别标有1、2、3、4的小球,它们的形状、大小等完全相同.小明先从口袋里随机不放回地取出一个小球,记下数字为x;小红在剩下有三个小球中随机取出一个小球,记下数字y,组成一对数(x,y).
(1)用列表法或树状图表示出(x,y)的所有可能的结果;
(2)求小明、小红各取出的小球所确定的一对是满足函数y=-x+5的概率.
(1)用列表法或树状图表示出(x,y)的所有可能的结果;
(2)求小明、小红各取出的小球所确定的一对是满足函数y=-x+5的概率.
考点:列表法与树状图法,一次函数图象上点的坐标特征
专题:计算题
分析:(1)先利用树状图展示所有12种等可能的结果数;
(2)根据一次函数图象上点的坐标特征判断12个点中哪些点满足要求,然后根据概率公式计算.
(2)根据一次函数图象上点的坐标特征判断12个点中哪些点满足要求,然后根据概率公式计算.
解答:解:(1)画树状图为:
共有12种等可能的结果数:(1,2)、(1,3)、(1,4)、(2,1)、(2,3)、(2,4)、(3,1)、(3,2)、(3,4)、(4,1)、(4,2)、(4,3);
(2)当x=1时,y=-x+5=4;当x=2时,y=-x+5=3;当x=3时,y=-x+5=2;当x=4时,y=-x+5=1,
则点(1,4)、(2,3)、(3,2),(4,1)在直线y=-x+5上,
所以小明、小红各取出的小球所确定的一对是满足函数y=-x+5的概率=
=
.

共有12种等可能的结果数:(1,2)、(1,3)、(1,4)、(2,1)、(2,3)、(2,4)、(3,1)、(3,2)、(3,4)、(4,1)、(4,2)、(4,3);
(2)当x=1时,y=-x+5=4;当x=2时,y=-x+5=3;当x=3时,y=-x+5=2;当x=4时,y=-x+5=1,
则点(1,4)、(2,3)、(3,2),(4,1)在直线y=-x+5上,
所以小明、小红各取出的小球所确定的一对是满足函数y=-x+5的概率=
| 4 |
| 12 |
| 1 |
| 3 |
点评:本题考查了列表法与树状图法:通过列表法或树状图法展示所有可能的结果求出n,再从中选出符合事件A或B的结果数目m,求出概率.也考查了一次函数图形上点的坐标特征.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在半径为2cm的⊙O内有长为2
cm的弦AB,由此弦所对的圆心角∠AOB为( )
| 3 |
| A、60° | B、90° |
| C、120° | D、150° |
下列说法正确的是( )
| A、0是最小的数 |
| B、互为相反数的两个数的和为0 |
| C、有理数分为整数、分数和0 |
| D、有理数分为非负有理数和正有理数 |
在下列命题中,正确的是( )
| A、邻边之比相等的两个平行四边形一定相似 |
| B、有一个角是70°两个等腰三角形一定相似 |
| C、两个直角三角形一定相似 |
| D、有一个角是60°的两个菱形一定相似 |
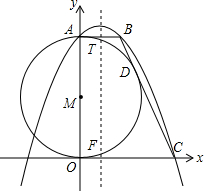 如图,在直角坐标系中,⊙M的圆心在y轴的正半轴上,AB与⊙M相切于A,BC与⊙M相切于点D,圆M与x轴相切于点O,已知B点坐标为(4,12).
如图,在直角坐标系中,⊙M的圆心在y轴的正半轴上,AB与⊙M相切于A,BC与⊙M相切于点D,圆M与x轴相切于点O,已知B点坐标为(4,12). 如图,在△ABC中,AD是边BC上的高,E为边AC的中点,BC=14,AD=12,sinB=
如图,在△ABC中,AD是边BC上的高,E为边AC的中点,BC=14,AD=12,sinB=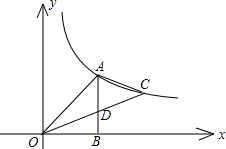 已知:如图,在平面直角坐标系xOy中,直线AC与反比例函数在第一象限内的图象交于点A、C,连接OA、OC,过点A作AB⊥x轴于点B,交OC于点D,且△AOB为等腰直角三角形,tan∠COB=
已知:如图,在平面直角坐标系xOy中,直线AC与反比例函数在第一象限内的图象交于点A、C,连接OA、OC,过点A作AB⊥x轴于点B,交OC于点D,且△AOB为等腰直角三角形,tan∠COB=