题目内容
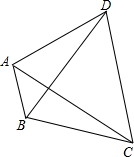 如图,已知∠ABC=120°,BD平分∠ABC,∠DAC=60°,若AB=2,BC=3,则BD的长是( )
如图,已知∠ABC=120°,BD平分∠ABC,∠DAC=60°,若AB=2,BC=3,则BD的长是( )| A、5 | B、7 | C、8 | D、9 |
考点:等边三角形的判定与性质,全等三角形的判定与性质
专题:
分析:在CB的延长线上取点E,使BE=AB,连接AE,则可证得△ABE为等边三角形,再结合条件可证明△ABD≌△AEC,可得BD=CE,再利用线段的和差可求得CE,则可求得BD.
解答: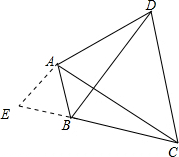 解:在CB的延长线上取点E,使BE=AB,连接AE,
解:在CB的延长线上取点E,使BE=AB,连接AE,
∵∠ABC=120°,
∴∠ABE=180-∠ABC=60°,
∵BE=AB,
∴△ABE为等边三角形,
∴AE=AB,∠BAE=∠E=60°,
∵∠DAC=60°,
∴∠DAC=BAE,
∵∠BAD=∠BAC+∠DAC,∠EAC=∠BAC+∠BAE,
∴∠BAD=∠EAC,
∵BD平分∠ABC,
∴∠ABD=
∠ABC=60°,
∴∠ABD=∠E,
在△ABD和△AEC中,
,
∴△ABD≌△AEC(ASA),
∴BD=CE,
∵CE=BE+BC=AB+BC=3+2=5,
∴BD=5,
故选A.
 解:在CB的延长线上取点E,使BE=AB,连接AE,
解:在CB的延长线上取点E,使BE=AB,连接AE,∵∠ABC=120°,
∴∠ABE=180-∠ABC=60°,
∵BE=AB,
∴△ABE为等边三角形,
∴AE=AB,∠BAE=∠E=60°,
∵∠DAC=60°,
∴∠DAC=BAE,
∵∠BAD=∠BAC+∠DAC,∠EAC=∠BAC+∠BAE,
∴∠BAD=∠EAC,
∵BD平分∠ABC,
∴∠ABD=
| 1 |
| 2 |
∴∠ABD=∠E,
在△ABD和△AEC中,
|
∴△ABD≌△AEC(ASA),
∴BD=CE,
∵CE=BE+BC=AB+BC=3+2=5,
∴BD=5,
故选A.
点评:本题主要考查等边三角形的判定和性质和全等三角形的判定和性质,构造△ABE再证△ABD≌△AEC是解题的关键.

练习册系列答案
相关题目
在半径为2cm的⊙O内有长为2
cm的弦AB,由此弦所对的圆心角∠AOB为( )
| 3 |
| A、60° | B、90° |
| C、120° | D、150° |
把代数式“
-5”用文字语言叙述,其中表述不正确的是( )
| 1 |
| x |
| A、比x的倒数小5的数 |
| B、x的倒数与5的差 |
| C、x与5的差的倒数 |
| D、1除以x的商与5的差 |
下列说法正确的是( )
| A、0是最小的数 |
| B、互为相反数的两个数的和为0 |
| C、有理数分为整数、分数和0 |
| D、有理数分为非负有理数和正有理数 |
 如图是个长方形花园,一只小鸟任意落下,掉进花园内,则小鸟在阴影区域内的概率是( )
如图是个长方形花园,一只小鸟任意落下,掉进花园内,则小鸟在阴影区域内的概率是( )A、
| ||
B、
| ||
C、
| ||
| D、不能确定 |
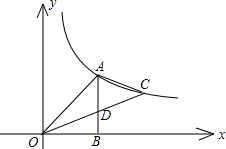 已知:如图,在平面直角坐标系xOy中,直线AC与反比例函数在第一象限内的图象交于点A、C,连接OA、OC,过点A作AB⊥x轴于点B,交OC于点D,且△AOB为等腰直角三角形,tan∠COB=
已知:如图,在平面直角坐标系xOy中,直线AC与反比例函数在第一象限内的图象交于点A、C,连接OA、OC,过点A作AB⊥x轴于点B,交OC于点D,且△AOB为等腰直角三角形,tan∠COB=