题目内容
5. 如图,OA、OB、OC分别是⊙O的半径,且AC=BC,D、E分别是OA、OB的中点,求证:CD=CE.
如图,OA、OB、OC分别是⊙O的半径,且AC=BC,D、E分别是OA、OB的中点,求证:CD=CE.
分析 根据圆心角、弧、弦的关系得到∠AOC=∠BOC,证明△DOC≌△EOC,根据全等三角形的性质证明结论.
解答 证明:∵AC=BC,
∴∠AOC=∠BOC,
∵D、E分别是OA、OB的中点,且OA=OB,
∴OD=OE,
在△DOC和△EOC中,
$\left\{\begin{array}{l}{OD=OE}\\{∠AOC=∠BOC}\\{OC=OC}\end{array}\right.$,
∴△DOC≌△EOC,
∴CD=CE.
点评 本题考查的是圆心角、弧、弦的关系和三角形全等的判定和性质,理解在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等是解题的关键.

练习册系列答案
相关题目
16.某商品连续两次降价.单价由100元降至81元,若两次的降价的百分率一样,则这样百分率为( )
| A. | 10% | B. | 20% | C. | 30% | D. | 40% |
13.已知x=2是关于x的一元二次方程x2-x+2a=0的一个解,则a的值为( )
| A. | 0 | B. | -1 | C. | 1 | D. | 2 |
10.据统计,徐州旅游业今年1至10月总收入71860 000 000元,这个数用科学记数法表示为( )
| A. | 7.186×1011元 | B. | 7.186×109元 | C. | 7.186×1010元 | D. | 7.186×108元 |
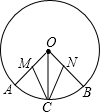 已知:如图OA,OB,OC是⊙O的半径,M,N分别为OA,OB的中点,且MC=NC,试判断$\widehat{AC}$和$\widehat{BC}$的关系,并说明理由.
已知:如图OA,OB,OC是⊙O的半径,M,N分别为OA,OB的中点,且MC=NC,试判断$\widehat{AC}$和$\widehat{BC}$的关系,并说明理由.