题目内容
15.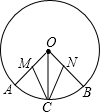 已知:如图OA,OB,OC是⊙O的半径,M,N分别为OA,OB的中点,且MC=NC,试判断$\widehat{AC}$和$\widehat{BC}$的关系,并说明理由.
已知:如图OA,OB,OC是⊙O的半径,M,N分别为OA,OB的中点,且MC=NC,试判断$\widehat{AC}$和$\widehat{BC}$的关系,并说明理由.
分析 由AM=20M,BN=20N,易得OM=ON,又由MC=NC,易证得△OMC≌ONC,则可得∠AOC=∠BOC,又由圆心角与弧的关系,即可证得结论.
解答 解:$\widehat{AC}$=$\widehat{BC}$,
理由:∵OA=OB,M,N分别为OA,OB的中点,
∴OM=ON,
在△OCM和△OCN中,
$\left\{\begin{array}{l}{OM=ON}\\{OC=OC}\\{MC=NC}\end{array}\right.$,
∴△OCM≌△OCN(SSS),
∴∠AOC=∠BOC,
∴$\widehat{AC}$=$\widehat{BC}$.
点评 此题考查了圆心角与弧的关系以及全等三角形的判定与性质,熟练掌握圆心角、弧、弦的关系是解题的关键.

练习册系列答案
相关题目
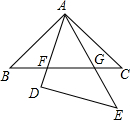 如图,△ABC与△DEA是两个全等的等腰直角三角形,∠BAC=∠D=90°,△DEA绕点A旋转,边AD、AE与BC分别与AD、AE相交于点F、G,CB=5.回答下列问题.
如图,△ABC与△DEA是两个全等的等腰直角三角形,∠BAC=∠D=90°,△DEA绕点A旋转,边AD、AE与BC分别与AD、AE相交于点F、G,CB=5.回答下列问题.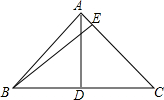 如图,在等腰△ABC中,AB=AC,底边上的高AD=10cm,腰AC上的高BE=12cm
如图,在等腰△ABC中,AB=AC,底边上的高AD=10cm,腰AC上的高BE=12cm
 如图,OA、OB、OC分别是⊙O的半径,且AC=BC,D、E分别是OA、OB的中点,求证:CD=CE.
如图,OA、OB、OC分别是⊙O的半径,且AC=BC,D、E分别是OA、OB的中点,求证:CD=CE.