题目内容
5.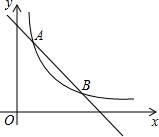 如图,在直角坐标系中,直线y=6-x与函数y=$\frac{5}{x}$(x>0)的图象交于A、B,设A(x1,y1),那么长为x1,宽为y1的矩形的面积和周长分别是5、12.
如图,在直角坐标系中,直线y=6-x与函数y=$\frac{5}{x}$(x>0)的图象交于A、B,设A(x1,y1),那么长为x1,宽为y1的矩形的面积和周长分别是5、12.
分析 此题首先要观察题目,求的是矩形的面积和周长,首先表示出矩形的面积:xy,正好符合反比例函数的特点,因此根据点A在反比例函数的图象上即可得解;然后求矩形的周长:2(x+y),此时发现周长的表达式正好符合直线AB的解析式,根据A点在直线AB的函数图象上即可得解.
解答 解:∵点A在函数y=$\frac{5}{x}$(x>0)上,
∴x1y1=5,
又∵点A在函数y=6-x上,
∴x1+y1=6,
∴矩形的周长为2(x1+y1)=12,
故答案为:5,12.
点评 此题主要考查了一次函数与反比例函数的交点问题,根据函数关系式中系数的意义直接求解,没必要求出交点坐标,难易程度适中.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
15.在△ABC和△A′B′C′中,∠B=∠B′,下列条件不能判断这两个三角形相似的是( )
| A. | ∠A=∠C′ | B. | ∠A=∠A′ | C. | $\frac{AB}{BC}=\frac{A′B′}{B′C′}$ | D. | $\frac{AB}{AC}=\frac{A′B′}{A′C′}$ |
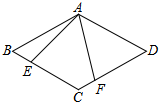 如图,菱形ABCD中,AB=4,∠ABC=60°,∠EAF=60°,∠EAF的两边分别交BC、CD于E、F两点,则CE+CF的值为( )
如图,菱形ABCD中,AB=4,∠ABC=60°,∠EAF=60°,∠EAF的两边分别交BC、CD于E、F两点,则CE+CF的值为( )
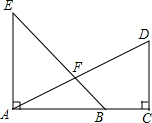 如图,已知AE⊥AC,DC⊥AC,AE=AC,AB=CD,AD与BE互相垂直且相等吗?为什么?
如图,已知AE⊥AC,DC⊥AC,AE=AC,AB=CD,AD与BE互相垂直且相等吗?为什么?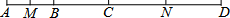 如图,AB:BC:CD=2:3:4,M是AB的中点,N是CD的中点,
如图,AB:BC:CD=2:3:4,M是AB的中点,N是CD的中点,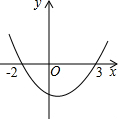 如图是抛物线y=ax2+bx+c的图象,则一元二次方程ax2+bx+c=0的解是x1=-2,x2=3.
如图是抛物线y=ax2+bx+c的图象,则一元二次方程ax2+bx+c=0的解是x1=-2,x2=3.