题目内容
已知,在△ABC中,AB=AC,直线m经过点A,点D,E是直线m上的动点,且∠BDE=∠AEC=∠BAC.
(1)如图1,求证:DE=BD+CE;
(2)如图2,以AB为边作等边三角形ABF,连接FC,FD,FE(D,A,E三点互不重合),若∠BAC=120°,试判断△DEF的形状,并说明理由.
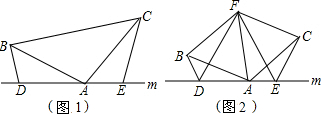
(1)如图1,求证:DE=BD+CE;
(2)如图2,以AB为边作等边三角形ABF,连接FC,FD,FE(D,A,E三点互不重合),若∠BAC=120°,试判断△DEF的形状,并说明理由.

考点:全等三角形的判定与性质
专题:
分析:(1)利用∠BDA=∠BAC得到:∠DBA+∠BAD=∠BAD+∠CAE,得出∠CAE=∠ABD,进而得出△ADB≌△CEA即可得出答案;
(2)由等边三角形ABF及∠BAC=120°,可得∠FAC=60°,由(1)知:△ADB≌△CEA,BD=AE,∠DBA=∠CAE,进而得出△FDB≌△FEA,所以FD=FE,∠BFD=∠AFE,进而得到∠DFE=60°,所以可判断△DEF的形状为等边三角形.
(2)由等边三角形ABF及∠BAC=120°,可得∠FAC=60°,由(1)知:△ADB≌△CEA,BD=AE,∠DBA=∠CAE,进而得出△FDB≌△FEA,所以FD=FE,∠BFD=∠AFE,进而得到∠DFE=60°,所以可判断△DEF的形状为等边三角形.
解答:证明:(1)证明:∵∠BDA=∠BAC,
∴∠DBA+∠BAD=∠BAD+∠CAE,
∴∠CAE=∠ABD,
在△ADB和△CEA中,
,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE;
(2)DF=EF.理由如下:

由(1)知,△ADB≌△CAE,
BD=EA,∠DBA=∠CAE,
∵△ABF为等边三角形,
∴∠ABF=∠BAF=60°,BF=AF,
∵∠BAC=120°,
∴∠FAC=60°,
∴∠DBA+∠ABF=∠CAE+∠CAF,
∴∠DBF=∠FAE,
在△DBF和△EAF中,
,
∴△DBF≌△EAF(SAS),
∴DF=EF,∠BFD=∠AFE,
∴∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°,
∴△DEF为等边三角形.
∴∠DBA+∠BAD=∠BAD+∠CAE,
∴∠CAE=∠ABD,
在△ADB和△CEA中,
|
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE;
(2)DF=EF.理由如下:

由(1)知,△ADB≌△CAE,
BD=EA,∠DBA=∠CAE,
∵△ABF为等边三角形,
∴∠ABF=∠BAF=60°,BF=AF,
∵∠BAC=120°,
∴∠FAC=60°,
∴∠DBA+∠ABF=∠CAE+∠CAF,
∴∠DBF=∠FAE,
在△DBF和△EAF中,
|
∴△DBF≌△EAF(SAS),
∴DF=EF,∠BFD=∠AFE,
∴∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°,
∴△DEF为等边三角形.
点评:本题考查了全等三角形的判定与性质:判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”;全等三角形的对应边相等.也考查了等边三角形的判定与性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 表示a、b的数在数轴上的位置如图,化简|2-a|+|b+2|的值为( )
表示a、b的数在数轴上的位置如图,化简|2-a|+|b+2|的值为( )| A、a+b | B、-a-b |
| C、a-b-4 | D、b-a+4 |
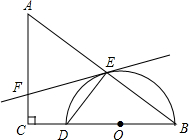 如图,在△ACB中,∠C=90°,AC=9,BC=12.O为BC边上一点,以O为圆心,OB为半径作半圆与BC边和AB边分别交于点D、点E,连结DE.
如图,在△ACB中,∠C=90°,AC=9,BC=12.O为BC边上一点,以O为圆心,OB为半径作半圆与BC边和AB边分别交于点D、点E,连结DE. 将△ABC向下平移5个单位长度.
将△ABC向下平移5个单位长度. 如图,某隧道的截面是一个半径为4.2米的半圆形,一辆高3.6米,宽3米的卡车能通过隧道吗?为什么?
如图,某隧道的截面是一个半径为4.2米的半圆形,一辆高3.6米,宽3米的卡车能通过隧道吗?为什么? 如图,BE,CF是△ABC的高,在BE上截取BP=AC,在CF的延长线上截取CQ=AB,求证:AP=AQ,∠QAP=90°.
如图,BE,CF是△ABC的高,在BE上截取BP=AC,在CF的延长线上截取CQ=AB,求证:AP=AQ,∠QAP=90°. 如图,在△ABC中,AB=AC,AD平分∠BAC,求证:DB=DC.
如图,在△ABC中,AB=AC,AD平分∠BAC,求证:DB=DC.