Question

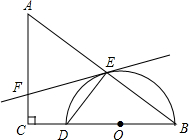如图，在△ACB中，∠C=90°，AC=9，BC=12．O为BC边上一点，以O为圆心，OB为半径作半圆与BC边和AB边分别交于点D、点E，连结DE．
（1）过点E作直线EF交AC边于F，当EF=AF时，求证：直线EF为半圆O的切线；
（2）当DE=4时，求圆的半径．

Answer 1

考点：切线的判定,相似三角形的判定与性质

专题：

分析：（1）连接OE．根据切线的判定定理，需证EF⊥OE；
（2）易证△ABC∽△DBE，得比例线段求解．

解答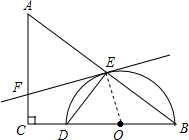：（1）证明：连接OE．
∵EF=AF，
∴∠A=∠AEF．
∵OE=OB，
∴∠OEB=∠OBE．
∵∠C=90°，
∴∠A+∠B=90°．
∴∠AEF+∠OEB=90°．
∴∠FEO=90°．
∵OE是⊙O半径，
∴EF是⊙O的切线．

（2）解：∵∠C=90°，BC=12，AC=9，
∴AB=15．
∵BD是直径，
∴∠DEB=90°．
∴∠DEB=∠C．
∵∠B=∠B，
∴△BED∽△BCA．
∴

BD

AB

=

DE

AC

，
∴

BD

15

=

4

9

，
解得：BD=

60

9

=

20

3

．

点评：本题考查了相似三角形的判定与性质，以及切线的判定，证明经过圆上一点的直线是圆的切线，常作辅助线是连接圆心和该点，证明直线和该半径垂直．