题目内容
用含a的代数式分别表示图1、图2、图3中阴影部分的面积.


考点:列代数式
专题:应用题
分析:根据图形,利用面积的和差计算不规则图形的面积:图1,S阴影部分=S正方形-S圆;图2,S阴影部分=S正方形-4S小圆;图3,S阴影部分=S正方形-9S小圆,然后利用正方形的面积公式和圆的面积公式进行表示即可.
解答:解:图1,S阴影部分=S正方形-S圆=a2-π•(
a)2=(1-
)a2;
图2,S阴影部分=S正方形-4S小圆=a2-4π•(
a)2=(1-
)a2;
图3,S阴影部分=S正方形-9S小圆=a2-9π•(
a)2=(1-
)a2.
| 1 |
| 2 |
| π |
| 4 |
图2,S阴影部分=S正方形-4S小圆=a2-4π•(
| 1 |
| 4 |
| π |
| 4 |
图3,S阴影部分=S正方形-9S小圆=a2-9π•(
| 1 |
| 6 |
| π |
| 4 |
点评:本题考查了列代数式:把问题中与数量有关的词语,用含有数字、字母和运算符号的式子表示出来,就是列代数式. 注意:要细辨别词义.,列代数式时,要先认真审题,抓住关键词语,仔细辩析词义.如“除”与“除以”,“平方的差(或平方差)”与“差的平方”的词义区分.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
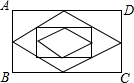 如图,矩形ABCD的长为4,宽为3,连续取三次中点后的最小四边形的面积是多少?
如图,矩形ABCD的长为4,宽为3,连续取三次中点后的最小四边形的面积是多少? 已知平行四边形ABCD的对角线相交于点O,BD=
已知平行四边形ABCD的对角线相交于点O,BD=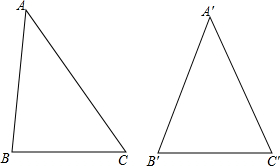 已知:两个等底等高的锐角三角形,可以将每个三角形分别分成四个三角形,分别涂上红色、蓝色、黄色和绿色,使得同色三角形全等.
已知:两个等底等高的锐角三角形,可以将每个三角形分别分成四个三角形,分别涂上红色、蓝色、黄色和绿色,使得同色三角形全等.