题目内容
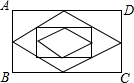 如图,矩形ABCD的长为4,宽为3,连续取三次中点后的最小四边形的面积是多少?
如图,矩形ABCD的长为4,宽为3,连续取三次中点后的最小四边形的面积是多少?考点:中点四边形
专题:计算题
分析:根据矩形的性质和中点四边形的性质得到矩形的中点四边形的面积为原矩形面积的一半,然后利用此结论计算即可.
解答:解:矩形ABCD的长为4,宽为3,取第1次中点后所得四边形的面积=
S矩形ABCD=
×3×4=6,
取第2次中点后所得中点四边形的面积=
×6=3,
取第3次中点后所得中点四边形的面积=
×3=
,
即连续取三次中点后的最小四边形的面积为
.
| 1 |
| 2 |
| 1 |
| 2 |
取第2次中点后所得中点四边形的面积=
| 1 |
| 2 |
取第3次中点后所得中点四边形的面积=
| 1 |
| 2 |
| 3 |
| 2 |
即连续取三次中点后的最小四边形的面积为
| 3 |
| 2 |
点评:本题考查了中点四边形:矩形的中点四边形为菱形,它的面积为原矩形面积的一半.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

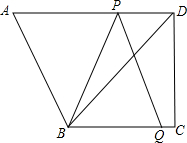 在直角梯形ABCD中,AD∥BC,∠C=90度,BC=16,AD=21,DC=12,动点P从点D出发,沿线段DA方向以每秒2个单位长度的速度运动,动点Q从点C出发,在线段CB以每秒1个单位长度的速度向点B运动.点P、Q同时出发,当点P运动到点A时,点Q随之停止运动,设运动时间为t秒.
在直角梯形ABCD中,AD∥BC,∠C=90度,BC=16,AD=21,DC=12,动点P从点D出发,沿线段DA方向以每秒2个单位长度的速度运动,动点Q从点C出发,在线段CB以每秒1个单位长度的速度向点B运动.点P、Q同时出发,当点P运动到点A时,点Q随之停止运动,设运动时间为t秒.
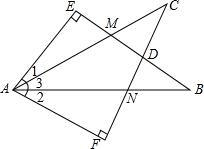 如图,已知在△ABE和△ACF中,∠E=∠F=90°,AB=AC,BE=CF.
如图,已知在△ABE和△ACF中,∠E=∠F=90°,AB=AC,BE=CF.