题目内容
1.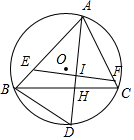 如图,△ABC内接于⊙O,I是△ABC的内心,延长AI交⊙O于D,连接BD,过I作直线EF分别交AB,AC于E,F,且AE=AF.
如图,△ABC内接于⊙O,I是△ABC的内心,延长AI交⊙O于D,连接BD,过I作直线EF分别交AB,AC于E,F,且AE=AF.(1)求证:以D为圆心,DB为半径的圆与EF相切;
(2)若BD=5,AD=9,BE•CF=4,求sin∠DBC的值.
分析 (1)只要证明DB=DI,DI⊥EF即可解决问题;
(2)由△EIB∽△FCI,推出EI•IF=BE•CF=4,推出EI=IF=2,由AD=9,BD=5,推出AI=9-5=4,在Rt△AIF中,AF=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,根据sin∠CBD=sin∠FAI=$\frac{IF}{AF}$,即可解决问题;
解答 (1)证明:如图,连接BI.
∵I是△ABC的内心,
∴∠IAB=∠IAC,
∠IBA=∠IBC,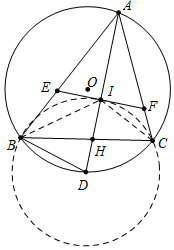
∵∠IAC=∠CBD,∠BID=∠IBA+∠IAB,∠DBI=∠CBD+∠IBC,
∴∠DBI=∠DIB,
∴DB=DI,
∵AE=AF,∠IAE=∠IAF,
∴AI⊥EF,即DI⊥EF,
∴以D为圆心,DB为半径的圆与EF相切.
(2)连接IC.
∵AE=AF,
∴∠AEF=∠AFE,
∴∠BEI=∠CFI,
∵∠EID=90°=∠EIB+∠BID=∠EIB+∠BAI+∠ABI,
又∵∠BAI+∠ABI+∠ICF=90°,
∴∠BIE=∠ICF,
∴△EIB∽△FCI,
∴EI•IF=BE•CF=4,
∴EI=IF=2,
∵AD=9,BD=5,
∴AI=9-5=4,
在Rt△AIF中,AF=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
∴sin∠CBD=sin∠FAI=$\frac{IF}{AF}$=$\frac{2}{2\sqrt{5}}$=$\frac{\sqrt{5}}{5}$.
点评 本题考查相似三角形的判定和性质、切线的判定和性质、三角形的内心、解直角三角形、锐角三角函数等知识,解题的关键是学会添加常用辅助线,正确寻找相似三角形解决问题,属于中考压轴题.

练习册系列答案
相关题目
9.在平面直角坐标系中,点P($\sqrt{(-2)^{2}}$,-2x2-1)所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
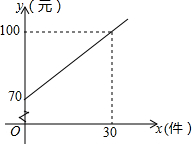 某快递公司的每位“快递小哥”日收入与每日的派送量成一次函数关系,如图所示.
某快递公司的每位“快递小哥”日收入与每日的派送量成一次函数关系,如图所示. 如图,平面直角坐标系中,已知直线y=x上一点P(2,2)C为y轴上一点,连接PC,线段PC绕点P顺时针旋转90°至线段PD,过点D作直线AB⊥x轴,垂足为B,直线AB与直线y=x交于点A,且BD=2AD,连接CD,直线CD与直线y=x交于点Q.
如图,平面直角坐标系中,已知直线y=x上一点P(2,2)C为y轴上一点,连接PC,线段PC绕点P顺时针旋转90°至线段PD,过点D作直线AB⊥x轴,垂足为B,直线AB与直线y=x交于点A,且BD=2AD,连接CD,直线CD与直线y=x交于点Q.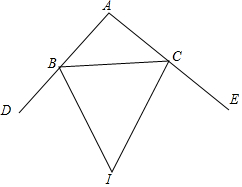 如图,BI,CI分别平分△ABC的外角∠DBC和∠ECB,
如图,BI,CI分别平分△ABC的外角∠DBC和∠ECB,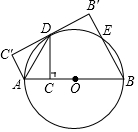 如图,AB是⊙O的直径,点C为AB上一点,作CD⊥AB交⊙O于D,连接AD,将△ACD沿AD翻折至△AC′D.
如图,AB是⊙O的直径,点C为AB上一点,作CD⊥AB交⊙O于D,连接AD,将△ACD沿AD翻折至△AC′D.