题目内容
14.某商品的进价为每件40元,售价为每件50元,每个月可卖出210件;如果每件商品的售价上涨1元,则每个月少卖10件(每件售价不能高于65元).设每件商品的售价上涨x元(x为正整数)月销售利润为y元,当x=5或6元时,最大利润y=2400元.分析 根据题意可知y=-10(x-5.5)2+2402.5,当x=5.5时y有最大值,再由题意得出x=5或6即可.
解答 解:由题意得:y=(210-10x)(50+x-40)
=-10x2+110x+2100(0<x≤15且x为整数);
=-10(x-5.5)2+2402.5.
∵a=-10<0,
∴当x=5.5时,y有最大值2402.5.
∵0<x≤15,且x为整数,
当x=5时,50+x=55,y=2400(元);
当x=6时,50+x=56,y=2400(元)
即当x=5元或6元时,每个月的利润最大,最大的月利润是2400元;
故答案为:5或6,2400.
点评 本题考查二次函数的实际应用以及配方法求最值;由题意得出销量与每件利润的关系式是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.在下列各数0.51515354…、0、0.80108、$\sqrt{4}$、0.2、3π、$\frac{22}{7}$、6.1010010001…、$\frac{131}{11}$、$\sqrt{7}$中,无理数的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
3.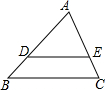 如图,在△ABC中,DE∥BC,AD=6,DB=3,则$\frac{{S}_{△ADE}}{{S}_{△ABC}}$的值为( )
如图,在△ABC中,DE∥BC,AD=6,DB=3,则$\frac{{S}_{△ADE}}{{S}_{△ABC}}$的值为( )
 如图,在△ABC中,DE∥BC,AD=6,DB=3,则$\frac{{S}_{△ADE}}{{S}_{△ABC}}$的值为( )
如图,在△ABC中,DE∥BC,AD=6,DB=3,则$\frac{{S}_{△ADE}}{{S}_{△ABC}}$的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{4}{9}$ |