题目内容
4.某学生在体育测试时推铅球,千秋所经过的路线是二次函数图象的一部分,如果这名学生出手处为A(0,2),铅球路线最高处为B(6,5),则该学生将铅球推出的距离是6+2$\sqrt{5}$.分析 由最高点的坐标可以设得二次函数的顶点坐标式,再将(0,2)代入即可求解.求得的函数解析式,令y=0,求得的x的正值即为铅球推出的距离.
解答 解:设二次函数的解析式为y=a(x-h)2+k,
由于顶点坐标为(6,5),
∴y=a(x-6)2+5.
又A(0,2)在抛物线上,
∴2=62•a+5,
解得:a=-$\frac{1}{12}$.
∴二次函数的解析式为y=-$\frac{1}{12}$(x-6)2+5,
整理得:y=-$\frac{1}{12}$x2+x+2.
当y=0时,-$\frac{1}{12}$x2+x+2=0.
x=6+2$\sqrt{15}$,x=6-2$\sqrt{15}$(不合题意,舍去).
∴x=6+2$\sqrt{15}$(米).
故答案为:6+2$\sqrt{15}$.
点评 本题考查了二次函数在实际生活中的应用,解题的关键是函数解析式的求法.

练习册系列答案
相关题目
19.等式$\sqrt{\frac{a}{a+2}}$=$\frac{\sqrt{a}}{\sqrt{a+2}}$成立的条件是( )
| A. | a≥0 | B. | a>-2 | C. | a≠-2 | D. | $\frac{a}{a+2}$≥0 |

 已知:如图,△ABC中,∠C=90°,∠A=30°,ED垂直平分AB交AB于点D,交AC于点E,EC=2.求AE的长.
已知:如图,△ABC中,∠C=90°,∠A=30°,ED垂直平分AB交AB于点D,交AC于点E,EC=2.求AE的长.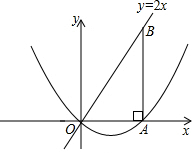 如图,在平面直角坐标系中,点B在直线y=2x上,过点B作x轴的垂线,垂足为A,OA=5,若抛物线y=x2+bx+c过O、A两点.
如图,在平面直角坐标系中,点B在直线y=2x上,过点B作x轴的垂线,垂足为A,OA=5,若抛物线y=x2+bx+c过O、A两点.