题目内容
10.已知一次函数y=bx+5和y=-x+a的图象交于点P(1,2),直接写出方程$\left\{\begin{array}{l}{bx-y=-5}\\{y+x=a}\end{array}\right.$的解$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$.分析 根据方程组的解即为函数图象的交点坐标解答即可.
解答 解:∵一次函数y=bx+5和y=-x+a的图象交于点P(1,2),
∴方程组$\left\{\begin{array}{l}{bx-y=-5}\\{y+x=a}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$.
故答案为为$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$.
点评 本题主要考查了一次函数与二元一次方程组,掌握函数图象交点坐标为两函数解析式组成的方程组的解是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.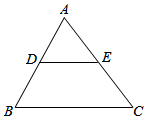 如图,三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=70°,∠B=70°,∠AED=30°,则∠C的度数是( )
如图,三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=70°,∠B=70°,∠AED=30°,则∠C的度数是( )
 如图,三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=70°,∠B=70°,∠AED=30°,则∠C的度数是( )
如图,三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=70°,∠B=70°,∠AED=30°,则∠C的度数是( )| A. | 20° | B. | 30° | C. | 40° | D. | 50° |
18.从A地到B地有一段上坡路和一段平路,如果车辆保持上坡每小时行驶30km,平路每小时行驶50km,下坡每小时行驶60km,那么车辆从A地到B地需要36分钟,从B地到A地需要21分钟,问A、B两地之间的坡路和平路各有多少千米?若设A、B两地之间的坡路为x km,平路为y km,根据题意可列方程组( )
| A. | $\left\{\begin{array}{l}{\frac{x}{30}+\frac{y}{50}=21}\\{\frac{x}{60}+\frac{y}{50}=36}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{\frac{x}{30}+\frac{y}{50}=36}\\{\frac{x}{60}+\frac{y}{50}=21}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{\frac{x}{30}+\frac{y}{50}=0.6}\\{\frac{x}{60}+\frac{y}{50}=0.35}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{\frac{x}{30}+\frac{y}{50}=0.35}\\{\frac{x}{60}+\frac{y}{50}=0.6}\end{array}\right.$ |
5.下列调查:①了解中央电视台“成语大赛”节目的收视率;②调查某城市居民家庭收入情况;③中国首个载货火箭“天舟一号”发射前对重要零部件的检查;④调查某种药品的药效.其中适合抽样调查的是( )
| A. | ①②③ | B. | ①②④ | C. | ②③④ | D. | ①③④ |
20.下列事件是必然事件的是( )
| A. | 经过不断的努力,每个人都能获得“星光大道”年度总冠军 | |
| B. | 小冉打开电视,正在播放“奔跑吧,兄弟” | |
| C. | 火车开到月球上 | |
| D. | 在十三名中国学生中,必有属相相同的 |
 如图,已知△ABC的面积为S,现将△ABC沿CA方向平移CA长度得到△AEF,则四边形CEFB的面积为3S.
如图,已知△ABC的面积为S,现将△ABC沿CA方向平移CA长度得到△AEF,则四边形CEFB的面积为3S. 如图,AC∥DF,AB∥EF,若∠2=50°,则∠1=50°.
如图,AC∥DF,AB∥EF,若∠2=50°,则∠1=50°.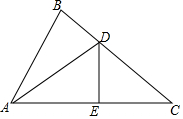 如图,已知∠BAC=60°,∠B=80°,DE垂直平分AC交BC于点D,交AC于E.
如图,已知∠BAC=60°,∠B=80°,DE垂直平分AC交BC于点D,交AC于E.