题目内容
5.已知:关于x的方程x2-(m+1)x+m-2=0有两异号实数根x1,x2,且x1>|x2|,若x12+x22=8.(1)求m的值;
(2)若函数y=x2+bx+c的图象与x轴的两个交点的横坐标为-x1+1,-x2+1.求当1≤x≤2时,函数y=|x2+bx+c|的最大值.
分析 (1)先根据一元二次方程根与系数的关系得到两根之和与两根之积,再把x12+x22转换为(x1+x2)2-2x1x2,然后利用前面的等式即可得到关于m的方程,解方程即可求出m的值;
(2)根据根与系数的关系可计算出b和c的值,则y=|x2+bx+c|变形为y=|x2+($\sqrt{3}$-1)x-2|或y=|x2-($\sqrt{3}$+1)x-2|,然后利用二次函数的性质在1≤x≤2确定函数的最大值.
解答 解:(1)根据题意得x1+x2=m+1,x1x2=m-2,
∵x12+x22=(x1+x2)2-2x1x2=8,
∴(m+1)2-2(m-2)=8,
整理得m2=3,解得m1=$\sqrt{3}$,m2=-$\sqrt{3}$.
∵△=(m+1)2-4(m-2)=(m-1)2+8>0,
∴m的值为$\sqrt{3}$或-$\sqrt{3}$.
(2)∵(-x1+1)+(-x2+1)=-b,(-x1+1)(-x2+1)=c,
∴b=x1+x2-2=m+1-2=m-1=±$\sqrt{3}$-1,
c=x1x2-(x1+x2)+1=m-2-m-1+1=-2,
∴y=|x2+bx+c|变形为y=|x2+($\sqrt{3}$-1)x-2|或y=|x2-($\sqrt{3}$+1)x-2|,
对于y=|x2+($\sqrt{3}$-1)x-2|,当1≤x≤2时,x=2,y有最大值2$\sqrt{3}$,
y=|x2-($\sqrt{3}$+1)x-2|,当1≤x≤2时,x=2,y有最大值2$\sqrt{3}$,
∴当1≤x≤2时,函数y=|x2+bx+c|的最大值为2$\sqrt{3}$.
点评 本题考查了抛物线与x轴的交点:利用二次函数的交点式:y=a(x-x1)(x-x2)(a,b,c是常数,a≠0)可直接得到抛物线与x轴的交点坐标(x1,0),(x2,0),且这两个交点为抛物线上的对称点.也考查了根的判别式和根与系数的关系.

| A. | 大于0 | B. | 等于-12或-6 | C. | 小于0 | D. | 最大值为12 |
①1$\frac{1}{3}$x2y;②ab÷c2;$③\frac{2m}{n}$;④2$\frac{a}{b}$;⑤2×a;⑥mb•4.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | x、(x-1) | B. | (x+1) | C. | x2-x | D. | 以上都是 |
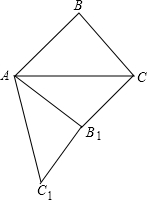 如图,在△ABC中,∠ABC=90°,AB=5,BC=4,将△ABC绕顶点A旋转到△AB1C1的位置(其中点B1对应点B,点C1对应点C),使得B1C∥AB,那么B1C=2.
如图,在△ABC中,∠ABC=90°,AB=5,BC=4,将△ABC绕顶点A旋转到△AB1C1的位置(其中点B1对应点B,点C1对应点C),使得B1C∥AB,那么B1C=2.