题目内容
15.已知关于x的一元二次方程ax2+bx+c=0的两根为α,β,且两个关于x的方程x2+(α+1)x+β2=0与x2+(β+1)x+α2=0有唯一的公共根,求a,b,c的关系式.分析 方程x2+(α+1)x+β2=0与x2+(β+1)x+α2=0连立方程组,两式做差可得(α-β)x-(α2-β2)=0,因为这两个方程有唯一的公共根,可得x=α+β,代入x2+(α+1)x+β2=0,再根据根与系数的关系得到a,b,c的关系式.
解答 解:$\left\{\begin{array}{l}{{x}^{2}+(α+1)x+{β}^{2}=0\\;\\;\\;\\;\\;\\;\\;\\;①}\\{{x}^{2}+(β+1)x+{α}^{2}=0\\;\\;\\;\\;\\;\\;\\;\\;②}\end{array}\right.$
①-②,得
(α-β)x-(α2-β2)=0
∵x2+(α+1)x+β2=0与x2+(β+1)x+α2=0有唯一的公共根
∴x=α+β
将x=α+β代入x2+(α+1)x+β2=0,得
(α+β)2+(α+1)(α+β)+β2=0
化简整理,得
2(α+β)2-αβ+(α+β)=0
∵一元二次方程ax2+bx+c=0的两根为α,β
∴$2×(-\frac{b}{a})^{2}-\frac{c}{a}+(-\frac{b}{a})=0$
整理,得
2b2-ac-ab=0
故答案为:a,b,c的关系式为:2b2-ac-ab=0.
点评 本题考查方程组的问题,根与系数的关系,两个方程组有唯一的公共根问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20. 如图,下面说法中错误的是( )
如图,下面说法中错误的是( )
 如图,下面说法中错误的是( )
如图,下面说法中错误的是( )| A. | 点B在直线MC上 | B. | 点A在直线BC外 | C. | 点C在线段MB上 | D. | 点M在线段BC上 |
7.在平面直角坐标系中,一次函数y=-2x-2的图象不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 如图,在△ABC中,∠C=90°,AD为∠BAC的平分线且DE⊥AB.若CD=3cm,则ED=3cm.
如图,在△ABC中,∠C=90°,AD为∠BAC的平分线且DE⊥AB.若CD=3cm,则ED=3cm.
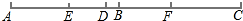 如图,已知线段AB和CD的公共部分BD=$\frac{1}{4}$AB=$\frac{1}{5}$CD,线段AB、CD的整点E、F之间距离是20cm,求BD的长.
如图,已知线段AB和CD的公共部分BD=$\frac{1}{4}$AB=$\frac{1}{5}$CD,线段AB、CD的整点E、F之间距离是20cm,求BD的长.