题目内容
如图，BC平分∠ABD，AB=12，BD=15，如果∠ACB=∠D，那么BC边的长为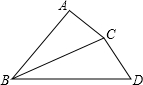
分析：先根据角平分线的性质求出△ABC∽△CBD，再根据相似三角形对应边成比例解答即可．
解答：解：∵BC平分∠ABD，
∴∠ABC=∠DBC，
又∵∠ACB=∠D，
∴△ABC∽△CBD，
∴
=
，AB=12，BD=15，
∴BC=
=
=6
．
∴∠ABC=∠DBC，
又∵∠ACB=∠D，
∴△ABC∽△CBD，
∴
| AB |
| BC |
| BC |
| BD |
∴BC=
| AB•BD |
| 12×15 |
| 5 |
点评：本题考查对相似三角形性质的理解，相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比．
练习册系列答案
相关题目
11、如图，BC平分∠DBA，∠1=∠2，填空：因为BC平分∠DBA，所以∠1=
5、如图，BC平分∠ABD，AB∥CD，点E在CD的延长线上，若∠C=27°，则∠BDE的度数为（ ）
如图，BC平分EF，BE=CF，求证：AB=AC．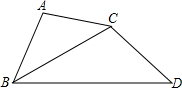
如图，BC平分∠ABD，AB=8，BD=18，若△ABC∽△CBD，则BC=