题目内容
 如图,BC平分EF,BE=CF,求证:AB=AC.
如图,BC平分EF,BE=CF,求证:AB=AC.分析:如图,作EM∥AC交BC于点M.易证△DEM≌△DFC(ASA),则推知EM=CF=EM,故∠B=∠EMB=∠ACB,所以由“等角对等边”得到AB=AC.
解答: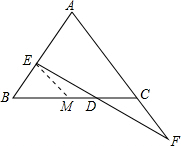 证明:如图,作EM∥AC交BC于点M.则∠MED=∠CFD,∠BME=∠ACB.
证明:如图,作EM∥AC交BC于点M.则∠MED=∠CFD,∠BME=∠ACB.
∵BC平分EF,
∴ED=FD,
∴在△DEM与△DFC中,
,
∴△DEM≌△DFC(ASA),
∴EM=CF.
又∵BE=CF,
∴BE=EM,
∴∠B=∠EMB,
∴∠B=∠ACB,
∴AB=AC.
 证明:如图,作EM∥AC交BC于点M.则∠MED=∠CFD,∠BME=∠ACB.
证明:如图,作EM∥AC交BC于点M.则∠MED=∠CFD,∠BME=∠ACB.∵BC平分EF,
∴ED=FD,
∴在△DEM与△DFC中,
|
∴△DEM≌△DFC(ASA),
∴EM=CF.
又∵BE=CF,
∴BE=EM,
∴∠B=∠EMB,
∴∠B=∠ACB,
∴AB=AC.
点评:本题考查了全等三角形的判定与性质.在应用全等三角形的判定时,要注意三角形间的公共边、公共角以及对顶角,必要时添加适当辅助线构造三角形.

练习册系列答案
相关题目
 (2012•重庆)已知:如图,BD平分∠ABC,点E在BC上,EF∥AB.若∠CEF=100°,则∠ABD的度数为( )
(2012•重庆)已知:如图,BD平分∠ABC,点E在BC上,EF∥AB.若∠CEF=100°,则∠ABD的度数为( ) 如图,BD平分∠ABC交AC于D,点E为CD上一点,且AD=DE,EF∥BC交BD于F.求证:AB=EF.
如图,BD平分∠ABC交AC于D,点E为CD上一点,且AD=DE,EF∥BC交BD于F.求证:AB=EF.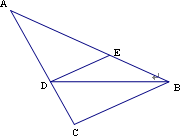
 如图,BC平分EF,BE=CF,求证:AB=AC.
如图,BC平分EF,BE=CF,求证:AB=AC.