题目内容
如图,一次函数y=ax+b与反比例函数y=
(x>0)的图象交于点A、B,与x、y轴交于C、D,且满足
+(a+
)2=0.
(1)求反比例函数解析式;
(2)当AB=BC时,求b的值;
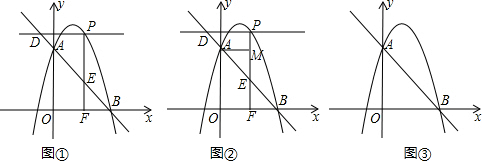
(3)如图2,当b=2
时,连OA,将OA绕点O逆时针旋转60°,使点A与点P重合,以点P为顶点作∠MPN=60°,分别交直线AB和x轴于点M、N,求证:PM平分∠AMN.

| k |
| x |
k-
|
| 3 |
(1)求反比例函数解析式;
(2)当AB=BC时,求b的值;
(3)如图2,当b=2
| 3 |

考点:反比例函数综合题,二次根式的性质与化简,反比例函数与一次函数的交点问题,全等三角形的判定与性质,等边三角形的判定与性质,相似三角形的判定与性质
专题:压轴题
分析:(1)由条件
+(a+
)2=0即可求出k和a,即可解决问题.
(2)过点A作AE⊥OC,垂足为E,过点B作BF⊥OC,垂足为F,如图1,设点A(m,
),通过三角形相似可以用m表示出点B的坐标,将点A、B的坐标代入直线AB的解析式,就可求出m和b的值.
(3)易证△OAC和△OAP都是等边三角形,结合∠MPN=60°可以证到△PON≌△PAE以及△POD≌△PAM,从而得到PN=PE,PD=PM,进而证到△PED≌△PNM.由这几组全等三角形就可得到∠PMA=∠PDO=∠PMN,则有PM平分∠AMN.
k-
|
| 3 |
(2)过点A作AE⊥OC,垂足为E,过点B作BF⊥OC,垂足为F,如图1,设点A(m,
| ||
| m |
(3)易证△OAC和△OAP都是等边三角形,结合∠MPN=60°可以证到△PON≌△PAE以及△POD≌△PAM,从而得到PN=PE,PD=PM,进而证到△PED≌△PNM.由这几组全等三角形就可得到∠PMA=∠PDO=∠PMN,则有PM平分∠AMN.
解答:(1)解:∵
+(a+
)2=0,
∴k-
=0,a+
=0,
解得:k=
,a=-
,
∴反比例函数解析式为:y=
.
(2)解:过点A作AE⊥OC,垂足为E,过点B作BF⊥OC,垂足为F,如图1,
设点A(m,
),
∵AE⊥OC,BF⊥OC,
∴AE∥BF.
∴△CFB∽△CEA.
∴
=
.
∵AB=BC,∴AC=2BC.
∴AE=2BF.
∴BF=
.
∴OF=
=2m.
∴点B(2m,
).
∵一次函数y=-
x+b与反比例函数y=
(x>0)的图象交于点A、B,
∴
.
解得:
.
∴b的值为
.
(3)证明:延长AO与射线PN交于点D,连接AP,过点A作AH⊥OC,垂足为H,如图2,
联立
.
解得:
.
∴点A的坐标为(1,
),OH=1,AH=
.
∴OA=2,∠AOH=60°.
由-
x+2
=0得x=2,则OC=2.
∴OA=OC.
∴△OAC是等边三角形.
∴∠OAC=60°,OA=AC.
∵OP=OA,∠AOP=60°,
∴△AOP是等边三角形.
∴OP=AP,∠PAO=∠OPA=60°.
∵∠NPM=60°,
∴∠NPM=∠OPA.
∴∠NPO=∠EPA.
∵∠PON=180°-∠AOP-∠AOC=60°,
∴∠PON=∠PAE.
在△PON和△PAE中,
∴△PON≌△PAE(ASA).
∴PN=PE.
同理可得:△POD≌△PAM.
∴PD=PM,∠PDO=∠PMA.
在△PED和△PNM中,
.
∴△PED≌△PNM(SAS).
∴∠PDE=∠PMN.
∴∠PMA=∠PMN.
∴PM平分∠AMN.
k-
|
| 3 |
∴k-
| 3 |
| 3 |
解得:k=
| 3 |
| 3 |
∴反比例函数解析式为:y=
| ||
| x |
(2)解:过点A作AE⊥OC,垂足为E,过点B作BF⊥OC,垂足为F,如图1,

设点A(m,
| ||
| m |
∵AE⊥OC,BF⊥OC,
∴AE∥BF.
∴△CFB∽△CEA.
∴
| BF |
| AE |
| BC |
| AC |
∵AB=BC,∴AC=2BC.
∴AE=2BF.
∴BF=
| ||
| 2m |
∴OF=
| ||||
|
∴点B(2m,
| ||
| 2m |
∵一次函数y=-
| 3 |
| ||
| x |
∴
|
解得:
|
∴b的值为
3
| ||
| 2 |
(3)证明:延长AO与射线PN交于点D,连接AP,过点A作AH⊥OC,垂足为H,如图2,
联立
|
解得:
|
∴点A的坐标为(1,
| 3 |
| 3 |
∴OA=2,∠AOH=60°.
由-
| 3 |
| 3 |
∴OA=OC.
∴△OAC是等边三角形.

∴∠OAC=60°,OA=AC.
∵OP=OA,∠AOP=60°,
∴△AOP是等边三角形.
∴OP=AP,∠PAO=∠OPA=60°.
∵∠NPM=60°,
∴∠NPM=∠OPA.
∴∠NPO=∠EPA.
∵∠PON=180°-∠AOP-∠AOC=60°,
∴∠PON=∠PAE.
在△PON和△PAE中,
|
∴△PON≌△PAE(ASA).
∴PN=PE.
同理可得:△POD≌△PAM.
∴PD=PM,∠PDO=∠PMA.
在△PED和△PNM中,
|
∴△PED≌△PNM(SAS).
∴∠PDE=∠PMN.
∴∠PMA=∠PMN.
∴PM平分∠AMN.
点评:本题考查了一次函数与反比例函数的交点问题、相似三角形的判定与性质、全等三角形的判定与性质、等边三角形的判定与性质、二次根式的性质等知识,综合性非常强,有一定的难度.而证出△POD≌△PAM和△PED≌△PNM是解决第三小题的关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
 如图,∠2=60°,若m∥n,则∠1的度数为( )
如图,∠2=60°,若m∥n,则∠1的度数为( )| A、30° | B、40° |
| C、60° | D、120° |
 在边长为2的正方形ABCD的边BC上,有一点P由B点向C点方向运动(P与C不重合),设PB=x,四边形APCD的面积为y,
在边长为2的正方形ABCD的边BC上,有一点P由B点向C点方向运动(P与C不重合),设PB=x,四边形APCD的面积为y, 已知,在Rt△OAB中,∠OAB中,∠OAB=90°,∠BOA=30°,OA=2
已知,在Rt△OAB中,∠OAB中,∠OAB=90°,∠BOA=30°,OA=2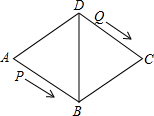 如图,菱形ABCD的边长为48cm,∠A=60°,动点P从点A出发,沿着线路AB-BD做匀速运动,动点Q从点D同时出发,沿着线路DC-CB-BA做匀速运动.
如图,菱形ABCD的边长为48cm,∠A=60°,动点P从点A出发,沿着线路AB-BD做匀速运动,动点Q从点D同时出发,沿着线路DC-CB-BA做匀速运动.