题目内容
20.已知0≤x≤$\frac{1}{2}$,那么函数y=-2x2+8x-6的最大值是-2.5.分析 把二次函数的解析式整理成顶点式形式,然后确定出最大值.
解答 解:∵y=-2x2+8x-6=-2(x-2)2+2.
∴该抛物线的对称轴是x=2,且在x<2上y随x的增大而增大.
又∵0≤x≤$\frac{1}{2}$,
∴当x=$\frac{1}{2}$时,y取最大值,y最大=-2($\frac{1}{2}$-2)2+2=-2.5.
故答案为-2.5.
点评 本题考查了二次函数的最值.确定一个二次函数的最值,首先看自变量的取值范围,当自变量取全体实数时,其最值为抛物线顶点坐标的纵坐标;当自变量取某个范围时,要分别求出顶点和函数端点处的函数值,比较这些函数值,从而获得最值.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
15.已知△ABC∽△DEF,且AB:DE=1:2,则△ABC与△DEF的周长之比为( )
| A. | 1:2 | B. | 2:1 | C. | 1:4 | D. | 4:3 |
9.估计$\sqrt{76}$的大小应在( )
| A. | 7~8之间 | B. | 9~10之间 | C. | 8.0~8.5之间 | D. | 8.5~9.0之间 |
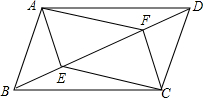 如图,?ABCD中,E、F两点都在对角线BD上,且BE=DF.求证:∠EAF=∠ECF.
如图,?ABCD中,E、F两点都在对角线BD上,且BE=DF.求证:∠EAF=∠ECF.
 如图所示的象棋盘上,若“士”的坐标是(-2,-2),“相”的坐标是(3,2),则“炮”的坐标是(-3,0).
如图所示的象棋盘上,若“士”的坐标是(-2,-2),“相”的坐标是(3,2),则“炮”的坐标是(-3,0). 如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,将Rt△ABC绕点A逆时针旋转45°后得到△AB′C′,点B经过的路径为$\widehat{BB′}$,图中阴影部分面积是( )
如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,将Rt△ABC绕点A逆时针旋转45°后得到△AB′C′,点B经过的路径为$\widehat{BB′}$,图中阴影部分面积是( )