题目内容
19.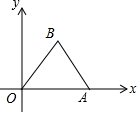 如图在平面直角坐标系中,等边三角形OAB的顶点A在x轴上,顶点B在第一象限,若OA=2,则点B关于原点的对称点坐标为( )
如图在平面直角坐标系中,等边三角形OAB的顶点A在x轴上,顶点B在第一象限,若OA=2,则点B关于原点的对称点坐标为( )| A. | (1,$\sqrt{3}$) | B. | ($\sqrt{3}$,1) | C. | (-1,-$\sqrt{3}$) | D. | (-$\sqrt{3}$,-1) |
分析 过点B作BC⊥x轴于C,根据等边三角形的性质可得OC=$\frac{1}{2}$OA,OB=OA,然后利用勾股定理列式求出BC,从而写出点B的坐标,再根据关于原点对称的点的横坐标与纵坐标都互为相反数解答.
解答  解:如图,过点B作BC⊥x轴于C,
解:如图,过点B作BC⊥x轴于C,
∵△OAB是等边三角形,
∴OC=$\frac{1}{2}$OA=$\frac{1}{2}$×2=1,OB=OA=2,
由勾股定理得,BC=$\sqrt{O{B}^{2}-O{C}^{2}}$=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
所以,点B的坐标为(1,$\sqrt{3}$),
∴点B关于原点的对称点坐标为(-1,-$\sqrt{3}$).
故选C.
点评 本题考查了等边三角形的性质,关于原点对称的点的坐标:关于原点的对称点,横纵坐标都变成相反数.

练习册系列答案
相关题目
7.$\sqrt{5}$的整数部分为m,小数部分是n,则($\sqrt{5}$+m)•n的值为( )
| A. | 0 | B. | 1 | C. | $\sqrt{5}$+1 | D. | $\sqrt{5}$-1 |
14.若方程x2-4x-3=0的两实根为x1、x2,则x1+x2的值为( )
| A. | -3 | B. | 3 | C. | -4 | D. | 4 |
11.若等腰三角形的周长为10,一边长为3,则这个等腰三角形的腰长为( )
| A. | 3.5 | B. | 3 | C. | 3.5或3 | D. | 6 |
9.下列方程是一元一次方程的是( )
| A. | 2x=-5 | B. | $\frac{2}{3}$x2=6 | C. | 3x-y=4 | D. | $\frac{4}{y}$+6=8 |
 已知:如图,AB=AC,AD=AE,∠1=∠2.求证:△ABD≌△ACE.
已知:如图,AB=AC,AD=AE,∠1=∠2.求证:△ABD≌△ACE. 设直线l1:y=-x+n的图象与y轴交于A点,直线l2:y=-3x-m的图象与y轴交于B点,l1与l2的图象相交于点C(-3,1).
设直线l1:y=-x+n的图象与y轴交于A点,直线l2:y=-3x-m的图象与y轴交于B点,l1与l2的图象相交于点C(-3,1).