题目内容
1. 如图:△ABC中,∠A=50°,BE平分∠ABC,CE是△ABC的外角∠ACD的角平分线,则∠E=25°.
如图:△ABC中,∠A=50°,BE平分∠ABC,CE是△ABC的外角∠ACD的角平分线,则∠E=25°.
分析 由题中角平分线可得∠E=∠ECF-∠EBC=$\frac{1}{2}$∠ACF-$\frac{1}{2}$∠ABC,进而得出∠A=180°-∠ABC-180°+∠ACF=∠ACF-∠ABC,即可得出结论.
解答 解:如图,∵EB、EC是∠ABC与∠ACF的平分线,
∴∠ECF=$\frac{1}{2}$∠ACF=∠E+∠EBC=∠E+$\frac{1}{2}$∠ABC,
∠E=∠ECF-∠EBC=$\frac{1}{2}$∠ACF-$\frac{1}{2}$∠ABC,
∠A=180°-∠ABC-∠ACB,
∠ACB=180°-∠ACF,
∴∠A=180°-∠ABC-180°+∠ACF=∠ACF-∠ABC,
又∵∠E=$\frac{1}{2}$∠ACF-$\frac{1}{2}$∠ABC,
∴∠E=$\frac{1}{2}$∠A=25°,
故答案为:25°
点评 本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.

练习册系列答案
相关题目
11.若等腰三角形的周长为10,一边长为3,则这个等腰三角形的腰长为( )
| A. | 3.5 | B. | 3 | C. | 3.5或3 | D. | 6 |
9.下列方程是一元一次方程的是( )
| A. | 2x=-5 | B. | $\frac{2}{3}$x2=6 | C. | 3x-y=4 | D. | $\frac{4}{y}$+6=8 |
6.下列事件是必然事件的是( )
| A. | 抛一枚硬币,正面朝上 | |
| B. | 通常加热到100℃,水沸腾 | |
| C. | 明天会下雪 | |
| D. | 经过某一有交通信号灯的路口恰好遇到红灯 |
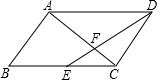 已知平行四边形ABCD中,点E是边BC的中点,DE与AC相交于点F,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,那么$\overrightarrow{FD}$=$\frac{1}{3}$$\overrightarrow{b}$-$\frac{2}{3}$$\overrightarrow{a}$ (用$\overrightarrow{a}$,$\overrightarrow{b}$的式子表示)
已知平行四边形ABCD中,点E是边BC的中点,DE与AC相交于点F,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,那么$\overrightarrow{FD}$=$\frac{1}{3}$$\overrightarrow{b}$-$\frac{2}{3}$$\overrightarrow{a}$ (用$\overrightarrow{a}$,$\overrightarrow{b}$的式子表示) 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3).
如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3).