题目内容
15. 如图,已知y=-2x+3的图象与y=x2的图象交于A、B两点且与x轴,y轴分别交于D、C两点,O为坐标轴原点.
如图,已知y=-2x+3的图象与y=x2的图象交于A、B两点且与x轴,y轴分别交于D、C两点,O为坐标轴原点.(1)求点A、B的坐标;
(2)求S△AOB的值.
分析 由题意可知,A、B两点的坐标就是一次函数y=-2x+3与二次函数y=x2连立方程组所得的公共解,作AE垂直与x轴与点E,则S△AOB=S△AED-S△AEO-S△BOD.
解答 解:(1)∵y=-2x+3的图象与y=x2的图象交于A、B两点,
∴解方程组$\left\{\begin{array}{l}{y=-2x+3}\\{y={x}^{2}}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{{x}_{1}=-3}\\{{y}_{1}=9}\end{array}\right.$ $\left\{\begin{array}{l}{{x}_{2}=1}\\{{y}_{2}=1}\end{array}\right.$
故点A的坐标为(-3,9),点B的坐标为(1,1).
(2)作AE垂直与x轴与点E,BF垂直与x轴与点F
将y=0代入y=-2x+3
得x=1.5,
∴点D的坐标为(1.5,0)
又∵点A的坐标为(-3,9),点B的坐标为(1,1)
∴${S}_{△AED}=\frac{|AE||ED|}{2}=\frac{9×4.5}{2}=\frac{81}{4}$,${S}_{△AEO}=\frac{|AE||EO|}{2}=\frac{9×3}{2}=\frac{27}{2}$,${S}_{△BOD}=\frac{|OD||BF|}{2}=\frac{1.5×1}{2}=\frac{3}{4}$
∴S△AOB=S△AED-S△AEO-S△BOD=$\frac{81}{4}-\frac{27}{2}-\frac{3}{4}=\frac{24}{4}=6$
故S△AOB的值为6.
点评 本题主要考查了抛物线与x轴交点的知识,解答本题的关键是求出A和B点的坐标,然后构造三角形,将所求的三角形面积进行转化求答.

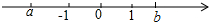
| A. | a<-a<b<-b<1 | B. | a<-b<b<1<-a | C. | a<b<-a<-b<1 | D. | a<-b<1<b<-a |
| A. | $\frac{1}{x}=1$ | B. | 2x-1=4 | C. | x2=y | D. | 2x2-x+1=0 |
| A. | y=5(x+3)2+2 | B. | y=5(x-3)2+2 | C. | y=5(x+3)2-2 | D. | y=5(x-3)2-2 |
 如图,△ABC≌△ADE,AB=AD,AC=AE,∠B=20°,∠E=110°,∠EAB=15°,则∠BAD的度数为65°.
如图,△ABC≌△ADE,AB=AD,AC=AE,∠B=20°,∠E=110°,∠EAB=15°,则∠BAD的度数为65°.
