题目内容
6.为了了解全校2500名学生对学校设置的体操、篮球、足球、跑步、舞蹈的课外体育活动项目的喜爱情况,在全校范围内随机抽取了若干名学生,对他们最喜爱的体育项目(每人只选一项)进行了问卷调查,将数据进行了统计并绘制成了如图所示的频率分布直方图和扇形统计图(均不完整)
(1)在这次问卷调查中,一共抽查了50名学生;
(2)补全频率分布直方图;
(3)估计该校2500名学生中有1000人最喜爱篮球活动;
(4)学校准备从随机调查中喜欢跑步和喜欢舞蹈的同学中分布任选一位参加体育活动总结会,若被随机调查的同学中,喜欢跑步的男同学有3名,喜欢舞蹈的女同学有2名,请用列表或画树状图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.
分析 (1)从扇形统计图中得到喜爱体操的百分比为10%,从条形统计图中得到喜爱体操的人数为5,则可利用百分比的意义可计算出抽查的总人数;
(2)先计算出喜爱篮球的人数,然后补全直方图;
(3)用样本中喜爱篮球的百分比表示全校喜爱篮球的百分比,然后乘以2500即可得到所有喜爱篮球的人数;
(4)先画树状图展示所有15种等可能的结果数,然后找出一位男同学和一位女同学的结果数后利用概率公式计算即可.
解答  解:(1)5÷10%=50(人).
解:(1)5÷10%=50(人).
所以在这次问卷调查中,一共抽查了50名学生;
(2)喜爱篮球的人数=50-5-17-5-3=20,
统计图为:
(3)2500×$\frac{20}{50}$=1000(人).
估计该校2500名学生中有1000人最喜爱篮球活动;
(4)画树状图为:
共有15种等可能的结果数,其中一位男同学和一位女同学的结果数为8,
所以一位男同学和一位女同学的概率=$\frac{8}{15}$.
故答案为50,1000.
点评 本题考查了列表法与树状图法:利用列表法和树状图法展示所有可能的结果求出n,再从中选出符合事件A或B的结果数目m,求出概率.也考查了样本估计整体和统计图.

练习册系列答案
相关题目
16.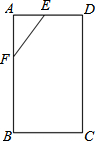 工人师傅砌门时,如图所示,常用木条EF固定矩形木框ABCD,使其不变形,这是利用( )
工人师傅砌门时,如图所示,常用木条EF固定矩形木框ABCD,使其不变形,这是利用( )
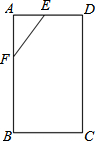 工人师傅砌门时,如图所示,常用木条EF固定矩形木框ABCD,使其不变形,这是利用( )
工人师傅砌门时,如图所示,常用木条EF固定矩形木框ABCD,使其不变形,这是利用( )| A. | 两点之间线段最短 | B. | 三角形的稳定性 | ||
| C. | 垂线段最短 | D. | 两直线平行,内错角相等 |
17.下列各数中最小的数是( )
| A. | -3 | B. | 3 | C. | 0 | D. | -$\frac{1}{3}$ |
1.已知:a=0.4,b=3,c=9,d=1.2,下列各式中,正确的是( )
| A. | $\frac{a}{b}$=$\frac{c}{d}$ | B. | $\frac{a}{c}$=$\frac{d}{b}$ | C. | $\frac{a}{b}$=$\frac{d}{c}$ | D. | $\frac{d}{c}$=$\frac{b}{a}$ |
 如图,在正方形网格上的一个△ABC.以P为一个顶点作与△ABC全等的三角形(规定点P与点B对应,另两顶点都在图中网格交点处),则可作出4个三角形与△ABC全等.
如图,在正方形网格上的一个△ABC.以P为一个顶点作与△ABC全等的三角形(规定点P与点B对应,另两顶点都在图中网格交点处),则可作出4个三角形与△ABC全等. 如图,已知y=-2x+3的图象与y=x2的图象交于A、B两点且与x轴,y轴分别交于D、C两点,O为坐标轴原点.
如图,已知y=-2x+3的图象与y=x2的图象交于A、B两点且与x轴,y轴分别交于D、C两点,O为坐标轴原点.