Question

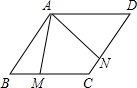如图，在?ABCD中，∠ABC=60°，AB=BC=4cm，点M，N分别在边BC，CD上，且∠MAN=60°，则四边形AMCN的面积为（　　）

• A、4

  3

  cm²
• B、2

  3

  cm²
• C、8

  3

  cm²
• D、8cm²

Answer 1

考点：平行四边形的性质

专题：

分析：根据图形的特点，连接AC，通过证明△ABM和△ANC全等可知阴影部分的面积正好等于平行四边形面积的一半．

解答：解：连接AC，
∵∠B=60°，
∴∠BAD=120°，
∵∠MAN=60°，
∴∠BAM=∠CAN，
∴△ABC为等边三角形，
∴AB=AC，
∴△ABM≌△ACN，
∴四边形AMCN的面积等于平行四边形面积的一半．
∵AB=4cm，
∴BC边上的高为2

3

，S_菱形ABCD=4×2

3

=8

3

∴四边形AMCN的面积等于

1

2

×8

3

=4

3

．
故选A．

点评：本题考查了等边三角形的判定和性质、平行四边形的性质、平行四边形的面积公式以及勾股定理的运用，题目比较简单．