题目内容
已知xy≠1,且7x2+2009x+13=0,13y2+2009y+7=0,求
的值.
| x |
| y |
考点:根与系数的关系
专题:计算题
分析:先把13y2+2009y+7=0变形得到7•(
)2+2009•
+13=0,由于xy≠1,7x2+2009x+13=0,所以x和
可看作方程7z2+2009z+13=0的两根,然后根据根与系数的关系求解.
| 1 |
| y |
| 1 |
| y |
| 1 |
| y |
解答:解:∵13y2+2009y+7=0,y≠0,
∴7•(
)2+2009•
+13=0,
而xy≠1,7x2+2009x+13=0,
∴x和
可看作方程7z2+2009z+13=0的两根,
∴x•
=
,
即
的值为
.
∴7•(
| 1 |
| y |
| 1 |
| y |
而xy≠1,7x2+2009x+13=0,
∴x和
| 1 |
| y |
∴x•
| 1 |
| y |
| 13 |
| 7 |
即
| x |
| y |
| 13 |
| 7 |
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程两个为x1,x2,则x1+x2=-
,x1•x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
已知正比例函数y=kx(k≠0)的图象经过点(1,2),则k的值为( )
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
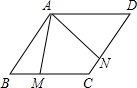 如图,在?ABCD中,∠ABC=60°,AB=BC=4cm,点M,N分别在边BC,CD上,且∠MAN=60°,则四边形AMCN的面积为( )
如图,在?ABCD中,∠ABC=60°,AB=BC=4cm,点M,N分别在边BC,CD上,且∠MAN=60°,则四边形AMCN的面积为( )A、4
| ||
B、2
| ||
C、8
| ||
| D、8cm2 |
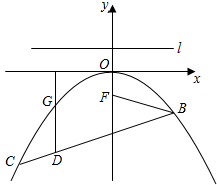 如图,抛物线y=ax2+bx+c关于y轴对称,它的顶点在坐标原点O,点B(2,-
如图,抛物线y=ax2+bx+c关于y轴对称,它的顶点在坐标原点O,点B(2,-