题目内容
如图，已知矩形ABCD，P、R分别是BC和DC上的点，E、F分别是PA、PR的中点，如果DR=3，AD=4，则EF的长为（ ）| A、2.5 | B、3 | C、4 | D、5 |
考点：三角形中位线定理,勾股定理
专题：
分析：利用勾股定理列式求出AR，再根据三角形的中位线平行于第三边并且等于第三边的一半可得EF=
AR．
| 1 |
| 2 |
解答：解：在矩形ABCD中，∠D=90°，
由勾股定理得，AR=
=
=5，
∵E、F分别是PA、PR的中点，
∴EF是△APR的中位线，
∴EF=
AR=
×5=2.5．
故选A．
由勾股定理得，AR=
| AD2+DR2 |
| 42+32 |
∵E、F分别是PA、PR的中点，
∴EF是△APR的中位线，
∴EF=
| 1 |
| 2 |
| 1 |
| 2 |
故选A．
点评：本题考查了三角形的中位线平行于第三边并且等于第三边的一半，勾股定理，熟记定理是解题的关键．
练习册系列答案
相关题目
如图，点D在AB的延长线上，∠A=35°，∠DBC=112°，则∠C的度数为
如图，E是?ABCD的一边AD上任意一点，若△EBC的面积为S1，?ABCD的面积为S，则S与S1的大小关系是（ ）A、S1=
| ||
B、S1＜
| ||
C、S1＞
| ||
| D、无法确定 |
已知正比例函数y=kx（k≠0）的图象经过点（1，2），则k的值为（ ）
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
用数轴表示不等式x-2＜0的解集正确的是（ ）
A、 |
B、 |
C、 |
D、 |
把一副三角板按如图叠放在一起，则∠α的度数是（ ）| A、165° | B、160° |
| C、155° | D、150° |
下列四个式子中，计算结果为1012的是（ ）
| A、106+106 |
| B、（210×510）2 |
| C、（2×5×105）×106 |
| D、（103）3 |
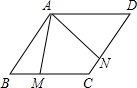如图，在?ABCD中，∠ABC=60°，AB=BC=4cm，点M，N分别在边BC，CD上，且∠MAN=60°，则四边形AMCN的面积为（ ）A、4
| ||
B、2
| ||
C、8
| ||
| D、8cm2 |