题目内容
10.已知关于x的一元二次方程x2-2x+m-1=0有两个实数根x1,x2.(1)求m的取值范围;
(2)当x12+x22=6x1x2时,求m的值.
分析 (1)根据一元二次方程x2-2x+m-1=0有两个实数根,可得△≥0,据此求出m的取值范围;
(2)根据根与系数的关系求出x1+x2,x1•x2的值,代入x12+x22=6x1x2求解即可.
解答 解:(1)∵原方程有两个实数根,
∴△=(-2)2-4(m-1)≥0,
整理得:4-4m+4≥0,
解得:m≤2;
(2)∵x1+x2=2,x1•x2=m-1,x12+x22=6x1x2,
∴(x1+x2)2-2x1•x2=6x1•x2,
即4=8(m-1),
解得:m=$\frac{3}{2}$.
∵m=$\frac{3}{2}$<2,
∴符合条件的m的值为$\frac{3}{2}$.
点评 本题考查了根与系数的关系以及根的判别式,解答本题的关键是掌握两根之和与两根之积的表达方式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.已知a2+3a=1,则代数式2a2+6a-1的值为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
2.一次数学测验中,某小组五位同学的成绩分别是:110,105,90,95,90,则这五个数据的中位数是( )
| A. | 90 | B. | 95 | C. | 100 | D. | 105 |
19.互为相反数的两个数的和为( )
| A. | 0 | B. | -1 | C. | 1 | D. | 2 |
 如图,已知抛物线y=$\frac{1}{3}$x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(-9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.
如图,已知抛物线y=$\frac{1}{3}$x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(-9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.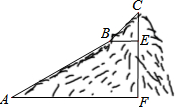 如图,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的,测得坡长AB=800米,BC=200米,坡角∠BAF=30°,∠CBE=45°.
如图,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的,测得坡长AB=800米,BC=200米,坡角∠BAF=30°,∠CBE=45°.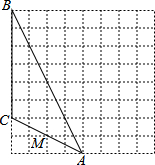 如图是一个由8×8个小正方形组成的方格纸,我们把顶点在正方形顶点的三角形称为格点三角形,图中的△ABC就是一个格点三角形,点M是AC的中点.
如图是一个由8×8个小正方形组成的方格纸,我们把顶点在正方形顶点的三角形称为格点三角形,图中的△ABC就是一个格点三角形,点M是AC的中点.