题目内容
5.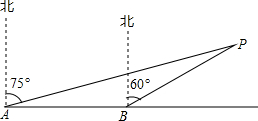 某轮船由西向东航行,在A处测得小岛P的方位是北偏东75°,又继续航行18海里后,在B处测得小岛P的方位是北偏东60°.
某轮船由西向东航行,在A处测得小岛P的方位是北偏东75°,又继续航行18海里后,在B处测得小岛P的方位是北偏东60°. (1)在图上标出已知条件中的两个方向角;
(2)若轮船教学航行,求轮船与小岛P的最近距离.
分析 (1)根据题意作出标注即可;
(2)过P作AB的垂线PD,在直角△BPD中可以求的∠PAD的度数是30度,即可证明△APB是等腰三角形,即可求解.
解答 解:(1)如图所示: ;
;
(2)解:过P作PD⊥AB于点D.
∵∠PBD=90°-60°=30°
且∠PBD=∠PAB+∠APB,∠PAB=90-75=15°
∴∠PAB=∠APB
∴BP=AB=18(海里)
答:若轮船教学航行,求轮船与小岛P的最近距离是18海里.
点评 本题考查了方向角和勾股定理的应用.解一般三角形的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.正确证明△APB是等腰三角形是解决本题的关键.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
16.点(3,4)是反比例函数y=$\frac{{m}^{2}+2m-1}{x}$图象上一点,则此函数图象必经过点( )
| A. | (3,-4) | B. | (2,-6) | C. | (4,-3) | D. | (2,6) |
16.在$\frac{x+1}{x+2}$,$\frac{m-3}{m}$,$\frac{a+3b}{5π}$,$\frac{4}{3-2x}$,$\frac{m-n}{4}$中分式的个数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
12.已知直角三角形的两直角边长分别是4和6,则其斜边长是( )
| A. | 4 | B. | 6 | C. | 10 | D. | 2$\sqrt{13}$ |
 如图,AD是△ABC的高,E是AC上一点,BE交AD于F,且有BD=AD,DF=DC,试说明BE⊥AC.
如图,AD是△ABC的高,E是AC上一点,BE交AD于F,且有BD=AD,DF=DC,试说明BE⊥AC. 如图,线段AB的垂直平分线l交AB于C点,点P在l上,PA=5,AC=4,则△PAB的周长为18.
如图,线段AB的垂直平分线l交AB于C点,点P在l上,PA=5,AC=4,则△PAB的周长为18.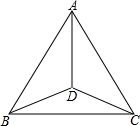 如图,点D是△ABC内部一点,AD平分∠BAC.
如图,点D是△ABC内部一点,AD平分∠BAC.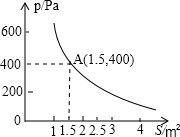 某校技小组进行野外考察,途中遇到一片十几米宽的烂泥湿地.为了安全、迅速通过这片湿地,他们沿着前进路线铺了若干块木块,构筑成一条临时近道.木板对地面的压强是木板面积的反比例函数,其图象如图所示
某校技小组进行野外考察,途中遇到一片十几米宽的烂泥湿地.为了安全、迅速通过这片湿地,他们沿着前进路线铺了若干块木块,构筑成一条临时近道.木板对地面的压强是木板面积的反比例函数,其图象如图所示