题目内容
16.在$\frac{x+1}{x+2}$,$\frac{m-3}{m}$,$\frac{a+3b}{5π}$,$\frac{4}{3-2x}$,$\frac{m-n}{4}$中分式的个数有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 判断分式的依据是看分母中是否含有字母,如果含有字母则是分式,如果不含有字母则不是分式.
解答 解:在$\frac{x+1}{x+2}$,$\frac{m-3}{m}$,$\frac{a+3b}{5π}$,$\frac{4}{3-2x}$,$\frac{m-n}{4}$中分式有$\frac{x+1}{x+2}$,$\frac{m-3}{m}$,$\frac{4}{3-2x}$,
分式的个数有3个.
故选:B.
点评 本题主要考查分式的定义,注意π不是字母,是常数,所以$\frac{a+3b}{5π}$不是分式,是整式.

练习册系列答案
相关题目
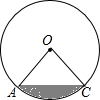 如图,⊙O的半径为2,$\widehat{AC}$的度数是90°,则图中阴影部分的面积是π-2.
如图,⊙O的半径为2,$\widehat{AC}$的度数是90°,则图中阴影部分的面积是π-2.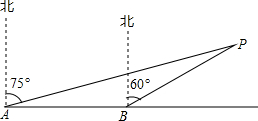 某轮船由西向东航行,在A处测得小岛P的方位是北偏东75°,又继续航行18海里后,在B处测得小岛P的方位是北偏东60°.
某轮船由西向东航行,在A处测得小岛P的方位是北偏东75°,又继续航行18海里后,在B处测得小岛P的方位是北偏东60°. 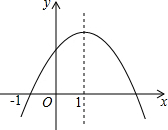 二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列结论:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列结论: 画出将三角形ABC绕点O顺时针方向旋转90度后的对应三角形.(保留作图痕迹)
画出将三角形ABC绕点O顺时针方向旋转90度后的对应三角形.(保留作图痕迹)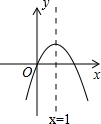 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:(1)b>0;(2)c>0;(3)4a+2b+c>0;(4)(a+b)2<b2,其中正确的有( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:(1)b>0;(2)c>0;(3)4a+2b+c>0;(4)(a+b)2<b2,其中正确的有( )