题目内容
14. 如图所示,在平面直角坐标系中,菱形MNPO的顶点P的坐标是(3,4),则顶点N的坐标分别是(8,4).
如图所示,在平面直角坐标系中,菱形MNPO的顶点P的坐标是(3,4),则顶点N的坐标分别是(8,4).
分析 由顶点P的坐标是(3,4),可求得OP的长,继而求得PN的长,又由四边形ABCD是菱形,求得答案.
解答 解:∵顶点P的坐标是(3,4),
∴OP=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵四边形ABCD是菱形,
∴OM=PN=5,PN∥OM,
∴顶点N的坐标分别是:(8,4).
故答案为:(8,4).
点评 此题考查了菱形的性质、勾股定理以及坐标与图形的性质.注意求得OP的长是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.下列各组数是勾股数的是( )
| A. | 32,42,52 | B. | 1.5,2,2.5 | C. | 6,8,10 | D. | $\sqrt{3}$,$\sqrt{4}$,$\sqrt{5}$ |
9.用配方法解下列方程,其中应在左右两边同时加上4的是( )
| A. | x2-2x=5 | B. | x2-8x=4 | C. | x2-4x-3=0 | D. | x2+2x=5 |
19.下列说法正确的是( )
| A. | 没有最大的正数,却有最大的负数 | B. | 数轴上离原点越远,表示数越大 | ||
| C. | 0大于一切负数 | D. | 在原点左边离原点越远,数就越大 |
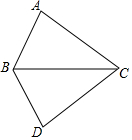 如图,∠ABC=∠DBC,请补充一个条件:AB=DB或∠A=∠D或∠ACB=∠DCB,使△ABC≌△DBC,并说明理由.
如图,∠ABC=∠DBC,请补充一个条件:AB=DB或∠A=∠D或∠ACB=∠DCB,使△ABC≌△DBC,并说明理由.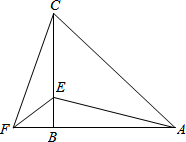 在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.
在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.