题目内容
 如图,在矩形ABCD中,AB=3cm,BC=4cm,△ABC沿AC翻折后点B落在B′,B′C与AD相交于点E,求△AEC的面积.
如图,在矩形ABCD中,AB=3cm,BC=4cm,△ABC沿AC翻折后点B落在B′,B′C与AD相交于点E,求△AEC的面积.考点:翻折变换(折叠问题)
专题:
分析:如图,首先证明∠EAC=∠ACE,得到AE=CE(设为λ),DE=4-λ;由勾股定理列出关于λ的方程,即可解决问题.
解答: 解:如图,由题意得:
解:如图,由题意得:
∠ACB=∠ACE;
∵四边形ABCD是矩形,
∴DC=AB=3,AD=BC=4;
∠D=90°,AD∥BC;
∴∠EAC=∠ACB,
∴∠EAC=∠ACE,
∴AE=CE(设为λ),则DE=4-λ;
由勾股定理得:λ2=32+(4-λ)2,
解得:λ=
,
∴△AEC的面积=
AE•CD
=
×
×3
=
.
 解:如图,由题意得:
解:如图,由题意得:∠ACB=∠ACE;
∵四边形ABCD是矩形,
∴DC=AB=3,AD=BC=4;
∠D=90°,AD∥BC;
∴∠EAC=∠ACB,
∴∠EAC=∠ACE,
∴AE=CE(设为λ),则DE=4-λ;
由勾股定理得:λ2=32+(4-λ)2,
解得:λ=
| 25 |
| 8 |
∴△AEC的面积=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 25 |
| 8 |
=
| 75 |
| 16 |
点评:该题主要考查了翻折变换的性质及其应用问题;解题的关键是灵活运用有关定理来分析、判断、推理或解答.

练习册系列答案
相关题目
 如图,△ABC的三个顶点都在⊙O上,连结CO、BO,已知∠A=55°,则∠BCO的度数是( )
如图,△ABC的三个顶点都在⊙O上,连结CO、BO,已知∠A=55°,则∠BCO的度数是( )| A、55° | B、45° |
| C、35° | D、30° |
2012年恩施机场和火车站的客流总量达到824000人次,这个数用科学记数法表示为( )
| A、824×104 |
| B、8.24×105 |
| C、8.24×106 |
| D、0.824×107 |


 如图,△ABC中,M为AC边的中点,E为AB上一点,且AE=
如图,△ABC中,M为AC边的中点,E为AB上一点,且AE=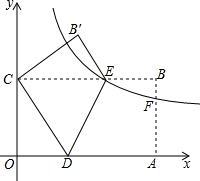 如图,在平面直角坐标系中,A(16,0)、C(0,8),四边形OABC是矩形,D、E分别是OA、B才边上的点,沿着DE折叠矩形,点A恰好落在y轴上的点C处,点B落在点B′处.
如图,在平面直角坐标系中,A(16,0)、C(0,8),四边形OABC是矩形,D、E分别是OA、B才边上的点,沿着DE折叠矩形,点A恰好落在y轴上的点C处,点B落在点B′处.