题目内容
4.已知抛物线的顶点是(4,2),且在x轴上截得的线段长为8,求此抛物线的解析式.分析 根据抛物线的对称性得到抛物线与x轴的两交点坐标为(0,0),(8,0),则可设交点式y=ax(x-8),然后把顶点坐标代入求出a即可.
解答 解:根据题意得抛物线的对称轴为直线x=4,
而抛物线在x轴上截得的线段长为8,
所以抛物线与x轴的两交点坐标为(0,0),(8,0),
设抛物线解析式为y=ax(x-8),
把(4,2)代入得a•4•(-4)=2,解得a=-$\frac{1}{8}$,
所以抛物线解析式为y=-$\frac{1}{8}$x(x-8),即y=-$\frac{1}{8}$x2+x.
点评 本题考查了待定系数法求二次函数的解析式:一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.本题的关键是利用对称性确定抛物线与x轴的交点坐标.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
14.如图,图案均是用长度相等的小木棒,按一定规律拼撘而成,第一个图案需4根小木棒,则第6个图案小木棒根数是( )


| A. | 42 | B. | 48 | C. | 54 | D. | 56 |
16.某商品连续两次降价.单价由100元降至81元,若两次的降价的百分率一样,则这样百分率为( )
| A. | 10% | B. | 20% | C. | 30% | D. | 40% |
13.已知x=2是关于x的一元二次方程x2-x+2a=0的一个解,则a的值为( )
| A. | 0 | B. | -1 | C. | 1 | D. | 2 |
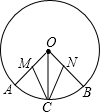 已知:如图OA,OB,OC是⊙O的半径,M,N分别为OA,OB的中点,且MC=NC,试判断$\widehat{AC}$和$\widehat{BC}$的关系,并说明理由.
已知:如图OA,OB,OC是⊙O的半径,M,N分别为OA,OB的中点,且MC=NC,试判断$\widehat{AC}$和$\widehat{BC}$的关系,并说明理由.