题目内容
6.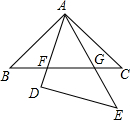 如图,△ABC与△DEA是两个全等的等腰直角三角形,∠BAC=∠D=90°,△DEA绕点A旋转,边AD、AE与BC分别与AD、AE相交于点F、G,CB=5.回答下列问题.
如图,△ABC与△DEA是两个全等的等腰直角三角形,∠BAC=∠D=90°,△DEA绕点A旋转,边AD、AE与BC分别与AD、AE相交于点F、G,CB=5.回答下列问题.(1)求证:△GAF∽△GBA;
(2)求证:AF2=FG•FC.
分析 (1)根据等腰直角三角形的性质得到∠C=∠B=∠DAE=∠E=45°,由外角的性质得到∠CFA=∠B+∠FAB,∠GAB=∠FAG+∠FAB,于是得到∠CFA=∠BAG,即可得到结论.
(2)方法同(1)证得△AGF∽△ACF,根据相似三角形的性质即可得到结论.
解答 证明:(1)∵△ABC与△DEA是两个全等的等腰直角三角形,∠BAC=∠EDA=90°,
∴∠C=∠B=∠DAE=∠E=45°,
∵∠CFA=∠B+∠FAB,∠GAB=∠FAG+∠FAB,
∴∠CFA=∠BAG,
∴△GAF∽△GBA;
(2)∵△ABC与△DEA是两个全等的等腰直角三角形,∠BAC=∠EDA=90°,
∴∠C=∠B=∠DAE=∠E=45°,
∵∠FGA=∠B+∠EAC,∠CAF=∠FAG+∠EAC,
∴∠AGF=∠CAF,
∴△AGF∽△ACF,
∴$\frac{AF}{FG}=\frac{CF}{AF}$,
∴AF2=FG•FC.
点评 本题考查了相似三角形的判定和性质,等腰直角三角形的性质,三角形外角的性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
16.下列各组数中,数值相等的是( )
| A. | 32和23 | B. | -23和(-2)3 | C. | -|23|和|-23| | D. | -32和(-3)2 |
14.如图,图案均是用长度相等的小木棒,按一定规律拼撘而成,第一个图案需4根小木棒,则第6个图案小木棒根数是( )


| A. | 42 | B. | 48 | C. | 54 | D. | 56 |
18.若$\frac{b}{a}$=0,则一定有( )
| A. | a≠0 | B. | a=b=0 | C. | a=0或b=0 | D. | b=0,a≠0 |
16.某商品连续两次降价.单价由100元降至81元,若两次的降价的百分率一样,则这样百分率为( )
| A. | 10% | B. | 20% | C. | 30% | D. | 40% |
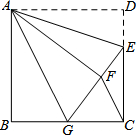 如图,在正方形ABCD中,AB=12,点E在边CD上,CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG,CF.有下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=6.其中正确的结论是①②③.
如图,在正方形ABCD中,AB=12,点E在边CD上,CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG,CF.有下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=6.其中正确的结论是①②③.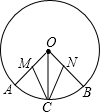 已知:如图OA,OB,OC是⊙O的半径,M,N分别为OA,OB的中点,且MC=NC,试判断$\widehat{AC}$和$\widehat{BC}$的关系,并说明理由.
已知:如图OA,OB,OC是⊙O的半径,M,N分别为OA,OB的中点,且MC=NC,试判断$\widehat{AC}$和$\widehat{BC}$的关系,并说明理由.