题目内容
13.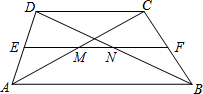 如图,在梯形ABCD中AB∥CD,中位线EF与对角线AC、BD交于M、N两点,若EF=18,NM=8,则AB长为( )
如图,在梯形ABCD中AB∥CD,中位线EF与对角线AC、BD交于M、N两点,若EF=18,NM=8,则AB长为( )| A. | 10 | B. | 13 | C. | 20 | D. | 26 |
分析 由梯形的中位线定理得出EF∥AB,E、F分别是AD、BC的中点,证出ME、NF、MF分别是△ADC、△BDC、△ABC的中位线,得出ME=NF=$\frac{1}{2}$CD,EN=$\frac{1}{2}$AB,求出EM,得出EN,即可得出AB的长.
解答 解:∵EF是梯形ABCD的中位线,
∴EF∥AB,E、F分别是AD、BC的中点,
∴M、N分别是AC、BD的中点,
∴ME、NF、MF分别是△ADC、△BDC、△ABC的中位线,
∴ME=NF=$\frac{1}{2}$CD,EN=$\frac{1}{2}$AB,
∴EM=$\frac{1}{2}$(EF-MN)=$\frac{1}{2}$(18-8)=5,
∴EN=5+8=13,∴AB=2EN=26;
故选:D.
点评 本题考查了梯形中位线定理、三角形中位线定理;熟练掌握梯形中位线和三角形中位线定理,并能进行推理论证与计算是解决问题的关键.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
3.为了简明扼要地说明某地区一天气温的变化情况,使用统计图最合适的是( )
| A. | 条形统计图 | B. | 折线统计图 | C. | 扇形统计图 | D. | 频数分布直方图 |
3.孔晓东同学在“低碳大武汉,绿色在未来”演讲比赛中,6位评委给他的打分如下表:
则他得分的中位数为90.
| 评委代号 | Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ | Ⅵ |
| 评 分 | 85 | 90 | 80 | 95 | 90 | 90 |
 如图,已知:AO=BO,CO=DO.试说明:
如图,已知:AO=BO,CO=DO.试说明: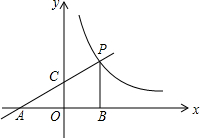 如图,一次函数y=$\frac{1}{2}$x+2的图象交x轴于点A,交y轴于点C,与反比例函数y=$\frac{m}{x}$(x>0)的图象交于点P,C为AP的中点,PB⊥x轴于点B
如图,一次函数y=$\frac{1}{2}$x+2的图象交x轴于点A,交y轴于点C,与反比例函数y=$\frac{m}{x}$(x>0)的图象交于点P,C为AP的中点,PB⊥x轴于点B