题目内容
1. 如图,已知:AO=BO,CO=DO.试说明:
如图,已知:AO=BO,CO=DO.试说明:(1)AD=BC;
(2)∠DAB=∠CBA.
分析 (1)根据SAS证明△ADO与△BCO全等,证明即可;
(2)根据全等三角形的性质得出∠DAO=∠CBO,再利用等式性质证明即可.
解答 证明:(1)在△ADO与△BCO中,
$\left\{\begin{array}{l}{AO=BO}\\{∠AOD=∠BOC}\\{CO=DO}\end{array}\right.$,
∴△ADO≌△BCO(SAS),
∴AD=BC;
(2)∵△ADO≌△BCO,
∴∠DAO=∠CBO,
∵OA=BO,
∴∠OAB=∠OBA,
∴∠DAB=∠CBA.
点评 此题考查全等三角形的判定和性质,关键是根据SAS证明△ADO与△BCO全等.

练习册系列答案
相关题目
11.某中学随机地调查了50名学生,了解他们一周在校的体育锻炼时间,结果如下表所示:
则这50名学生这一周在校的平均体育锻炼时间是6.4小时.
| 时间(小时) | 5 | 6 | 7 | 8 |
| 人数 | 10 | 15 | 20 | 5 |
13.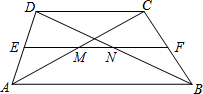 如图,在梯形ABCD中AB∥CD,中位线EF与对角线AC、BD交于M、N两点,若EF=18,NM=8,则AB长为( )
如图,在梯形ABCD中AB∥CD,中位线EF与对角线AC、BD交于M、N两点,若EF=18,NM=8,则AB长为( )
 如图,在梯形ABCD中AB∥CD,中位线EF与对角线AC、BD交于M、N两点,若EF=18,NM=8,则AB长为( )
如图,在梯形ABCD中AB∥CD,中位线EF与对角线AC、BD交于M、N两点,若EF=18,NM=8,则AB长为( )| A. | 10 | B. | 13 | C. | 20 | D. | 26 |
11.若x1、x2是一元二次方程x2-4x-3=0的两个根,则x1+x2的值是( )
| A. | -4 | B. | 4 | C. | 3 | D. | -3 |
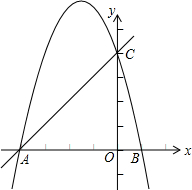 如图,抛物线y=ax2-bx-4a交x轴于点A、B,交y轴于点C,其中点B、C的坐标分别为B(1,0)、C(0,4).
如图,抛物线y=ax2-bx-4a交x轴于点A、B,交y轴于点C,其中点B、C的坐标分别为B(1,0)、C(0,4).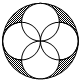 如图,四个半径为1的小圆都过大圆圆心且与大圆相内切,则阴影部分的面积为2π-4.
如图,四个半径为1的小圆都过大圆圆心且与大圆相内切,则阴影部分的面积为2π-4.