题目内容
2.在平面直角坐标系xOy中,⊙O的半径为4,点P的坐标为(3,4),则点P的位置为( )| A. | 在⊙O外 | B. | 在⊙O上 | C. | 在⊙O内 | D. | 不确定 |
分析 由勾股定理等性质算出点与圆心的距离d,则d>r时,点在圆外;当d=r时,点在圆上;当d<r时,点在圆内.
解答 解:由勾股定理,得
OP=$\sqrt{{3}^{2}+{4}^{2}}$=5>4,
即d>r,
点P在⊙O外,
故选:A.
点评 本题考查了对点与圆的位置关系的判断.关键要记住若半径为r,点到圆心的距离为d,则有:当d>r时,点在圆外;当d=r时,点在圆上,当d<r时,点在圆内.

练习册系列答案
相关题目
13.下列各组线段能构成直角三角形的一组是( )
| A. | 2,3,4 | B. | 6,8,11 | C. | 1,1,$\sqrt{2}$ | D. | 5,12,23 |
11.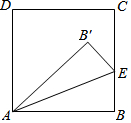 如图,将正方形ABCD的一角折叠,折痕为AE,∠B′AD比∠B′AE大48°,设∠B′AE和∠B′AD的度数分别为x、y,那么x、y所适合的一个方程组是( )
如图,将正方形ABCD的一角折叠,折痕为AE,∠B′AD比∠B′AE大48°,设∠B′AE和∠B′AD的度数分别为x、y,那么x、y所适合的一个方程组是( )
 如图,将正方形ABCD的一角折叠,折痕为AE,∠B′AD比∠B′AE大48°,设∠B′AE和∠B′AD的度数分别为x、y,那么x、y所适合的一个方程组是( )
如图,将正方形ABCD的一角折叠,折痕为AE,∠B′AD比∠B′AE大48°,设∠B′AE和∠B′AD的度数分别为x、y,那么x、y所适合的一个方程组是( )| A. | $\left\{\begin{array}{l}y-x=48\\ y+x=90\end{array}\right.$ | B. | $\left\{\begin{array}{l}y-x=48\\ y=2x\end{array}\right.$ | C. | $\left\{\begin{array}{l}y-x=48\\ y+2x=90\end{array}\right.$ | D. | $\left\{\begin{array}{l}x-y=48\\ y+2x=90\end{array}\right.$ |
12.在平面直角坐标系中,若点A (a,-b)在第一象限内,则点B (a,b-3)所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |