题目内容
12.解不等式组$\left\{\begin{array}{l}{3x+2>x}\\{\frac{1}{2}x≤2}\end{array}\right.$.分析 首先解每个不等式,两个不等式的解集的公共部分就是不等式组的解集.
解答 解:$\left\{\begin{array}{l}{3x+2>x…①}\\{\frac{1}{2}x≤2…②}\end{array}\right.$,
解①得x>-1,
解②得x≤4.
则不等式组的解集是-1<x≤4.
点评 本题考查了一元一次不等式组的解法,一般先求出其中各不等式的解集,再求出这些解集的公共部分,解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.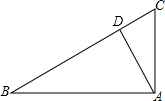 如图,在△ABC中,∠BAC=90°,∠B=30°,AC=5cm,AD⊥BC于D,则BD=( )
如图,在△ABC中,∠BAC=90°,∠B=30°,AC=5cm,AD⊥BC于D,则BD=( )
 如图,在△ABC中,∠BAC=90°,∠B=30°,AC=5cm,AD⊥BC于D,则BD=( )
如图,在△ABC中,∠BAC=90°,∠B=30°,AC=5cm,AD⊥BC于D,则BD=( )| A. | 10cm | B. | 7.5cm | C. | 8.5cm | D. | 6.5cm |
4.合肥市坚持以转变经济发展方式为主线,强化创新驱动,经济发展稳中有进,2015年前三季度,合肥市GDP超过3770亿元,3770亿用科学记数法可表示为( )
| A. | 3.77×103 | B. | 3.77×1010 | C. | 3.77×1011 | D. | 3.77×1012 |
1. 如图,已知正五边形ABCDE,AF∥CD,交DB的延长线于点F,则∠DFA等于( )
如图,已知正五边形ABCDE,AF∥CD,交DB的延长线于点F,则∠DFA等于( )
 如图,已知正五边形ABCDE,AF∥CD,交DB的延长线于点F,则∠DFA等于( )
如图,已知正五边形ABCDE,AF∥CD,交DB的延长线于点F,则∠DFA等于( )| A. | 30° | B. | 36° | C. | 45° | D. | 32° |
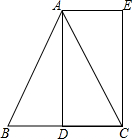 已知,如图,△ABC中,AB=AC,AD是BC边上的中线,AE∥BC,CE⊥AE;垂足为E.
已知,如图,△ABC中,AB=AC,AD是BC边上的中线,AE∥BC,CE⊥AE;垂足为E.