题目内容
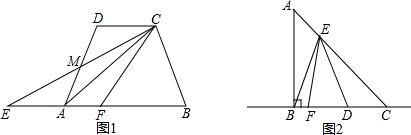
5．
如图，两个正方形边长分别是10厘米和6厘米，求阴影部分的面积．
分析 连接BD，则阴影部分的面积=△ABD的面积+扇形EBD的面积-△EBD的面积，求出ABD的面积、△ABE的面积和扇形的面积，即可得出结果．
解答 
解：连接BD，如图所示：
∵△ABD的面积=$\frac{1}{2}$AB×CD=$\frac{1}{2}$×10×6=30，
△BED的面积=$\frac{1}{2}$×6×6=18，
扇形EBD的面积=$\frac{1}{4}$π×62=9π，
∴阴影部分的面积=30+9π-18=12+9π．
点评 本题考查了正方形的性质、阴影面积的计算方法、三角形面积和扇形面积的计算；关键是将阴影部分的面积进行分割，再分别求出各个部分的面积即可．
练习册系列答案
智能训练练测考系列答案
相关题目
16．已知2a=3，2b=6，2c=12，则a，b，c之间满足的关系是（ ）
| A． | a+b=c | B． | ab=c | C． | 2b=a+c | D． | 无法确定 |
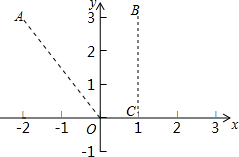对于两个已知图形G1、G2，在G1上任取一点P，在G2上任取一点Q，当线段PQ的长度最小时，我们称这个最小的长度为G1、G2的“密距”．如图，A（-2，3），B（1，3），C（1，0），则点A与射线OC之间的“密距”为$\sqrt{13}$，点B与射线OC之间的“密距”为3，如果直线y=x-1和双曲线y=$\frac{k}{x}$之间的“密距”为$\frac{3\sqrt{2}}{2}$，则k的值为-4．
10．在同一平面直角坐标系中，直线y=x与双曲线y=-$\frac{1}{x}$的交点个数为（ ）
| A． | 0个 | B． | 1个 | C． | 2个 | D． | 不能确定 |
