题目内容
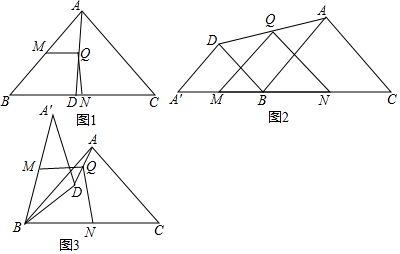
19.已知:等腰△ABC和等腰△DBA′共顶点B,其中AB=AC=A′B,DB=DA′,N为BC中点,M为A′B中点,将△DBA′绕点B逆时针旋转,连结AD,点Q为AD中点,连接QM,QN.(1)如图1,当点D落在BC上,BA与BA′重合时,求证:QM=QN;
(2)如图2,当A′、B、C在一条直线上时,(1)中的结论是否仍成立?请说明理由;
(3)△DBA′从图1位置向图2位置旋转过程中QM与QN是否始终相等?请结合图3说明理由.
分析 (1)如图1中,连接BQ,延长BQ到H,使得BQ=QH,连接AH、HC、DH.只要证明四边形ABDH是平行四边形,△AHC≌△HAD,推出AH=HC,再利用三角形中位线定理即可解决问题;
(2)(1)中的结论仍成立.理由梯形的中位线定理即可证明;
(3)结论:△DBA′从图1位置向图2位置旋转过程中QM与QN始终相等.如图3中,连接BQ,延长BQ到H,使得BQ=QH,连接AH、HC、DH、A′H,延长BD交AC于G,设A′D交AB于T.只要证明△A′HD≌△HAC,再利用三角形中位线定理即可解决问题;
解答 (1)证明:如图1中,连接BQ,延长BQ到H,使得BQ=QH,连接AH、HC、DH.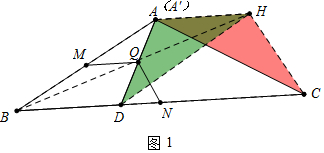
∵AQ=QD,BQ=QH,
∴四边形ABDH是平行四边形,
∴AH=BD,AH∥BC,∠AHD=∠ABD,
∴∠HAC=∠ACB=∠ABC,
∴∠AHD=∠HAC,
∵AC=AB=DH,AH=HA,
∴△AHD≌△HAC,
∴HC=AD=BD=AH,
∵BM=AM,BQ=QH,
∴MQ=$\frac{1}{2}$AH,
∵BN=NC,BQ=QH,
∴QN=$\frac{1}{2}$HC,
∵AH=HC,
∴QM=QN.
(2)解:结论:(1)中的结论仍成立.
理由:如图2中,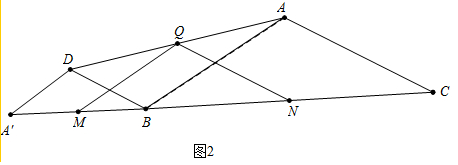
∵∠ABC=∠DA′B,∠DBA′=∠C,
∴DA′∥AB,BD∥AC,
∵DQ=QA,A′M=MB,BN=NC,
∴QM=$\frac{1}{2}$(A′D+AB),QN=$\frac{1}{2}$(BD+AC),
∵DA′=DB,AB=AC,
∴QM=QN.
(3)结论:△DBA′从图1位置向图2位置旋转过程中QM与QN始终相等.
理由:如图3中,连接BQ,延长BQ到H,使得BQ=QH,连接AH、HC、DH、A′H,延长BD交AC于G,设A′D交AB于T.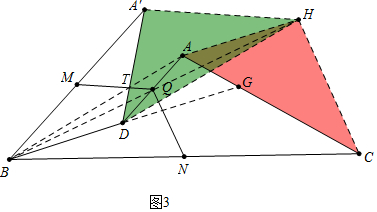
∵AQ=QD,BQ=QH,
∴四边形ABDH是平行四边形,
∴AH=BD=DA′,AH∥BD,
∴∠HAC=∠AGB=∠GBC+∠GCB,
∴∠A′DH=∠A′TH=∠A′BT+∠BA′D,
∵∠A′BT=∠GBC,∠BA′D=∠GCB,
∴∠A′DH=∠HAC,
∵AC=AB=DH,AH=BD=A′D,
∴△A′HD≌△HAC,
∴HC=A′H,
∵BM=A′M,BQ=QH,
∴MQ=$\frac{1}{2}$A′H,
∵BN=NC,BQ=QH,
∴QN=$\frac{1}{2}$HC,
∵A′H=HC,
∴QM=QN.
点评 本题考查几何变换综合题、等腰三角形的性质、全等三角形的判定和性质.平行四边形的判定和性质、三角形的中位线定理、梯形的中位线定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.

| x | -1 | 0 | 1 | 2 | 3 |
| y | 5 | 1 | -1 | -1 | 1 |
 正六边形ABCDE在平面直角坐标系内的位置如图所示,点A的坐标为(-2,0),点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,经过2017次翻转之后,点B的坐标是(4032,0).
正六边形ABCDE在平面直角坐标系内的位置如图所示,点A的坐标为(-2,0),点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,经过2017次翻转之后,点B的坐标是(4032,0). 如图,在?ABCD中,点E、F分别在边AB、CD 上,连接DE、BF,∠EDC=∠FBA.求证:四边形DEBF是平行四边形.
如图,在?ABCD中,点E、F分别在边AB、CD 上,连接DE、BF,∠EDC=∠FBA.求证:四边形DEBF是平行四边形.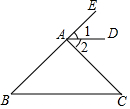 如图,已知AD∥BC,∠1=∠2,问∠B和∠C相等吗?为什么?
如图,已知AD∥BC,∠1=∠2,问∠B和∠C相等吗?为什么?