题目内容
9.已知单项式2x3ym-1与$\frac{1}{5}$xm-2ny4是同类项,求代数式:$\frac{2}{3}$(m-2n)-2(2n-m)+m-5的值.分析 根据同类项的定义得到m-2n=3,m-1=4,然后解方程组$\left\{\begin{array}{l}{m-2n=3}\\{m-1=4}\end{array}\right.$求得m,n,再化简$\frac{2}{3}$(m-2n)-2(2n-m)+m-5,把方程组的解代入进行计算即可.
解答 解:∵单项式2x3ym-1与$\frac{1}{5}$xm-2ny4是同类项,
∴$\left\{\begin{array}{l}{m-2n=3}\\{m-1=4}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=5}\\{n=1}\end{array}\right.$,
∴$\frac{2}{3}$(m-2n)-2(2n-m)+m-5
=$\frac{2}{3}$m-$\frac{4}{3}$n-4n+2m+m-5
=$\frac{11}{3}$m-$\frac{16}{3}$n-5
=$\frac{11}{3}$×5-$\frac{16}{3}$-5
=8.
点评 本题考查了整式的加减-化简求值,同类项的定义:所含字母相同,并且相同字母的次数也分别相同的项叫同类项.

练习册系列答案
相关题目
18.若$\sqrt{x+3}$=2,则(x+3)2的平方根是( )
| A. | 4 | B. | 8 | C. | ±4 | D. | ±8 |
1.二次函数y=ax2+bx+c图象上部分点的坐标满足如表:
则该函数图象过点( )
| x | … | -3 | -2 | -1 | 0 | 1 | … |
| y | … | -3 | -2 | -3 | -6 | -11 | … |
| A. | (-4,-6) | B. | (-4,-3) | C. | (-5,-2) | D. | (-5,-3) |
18.从2开始,连续的偶数相加,它们和的情况如表:
(1)若n=8时,则和S的值为56;(直接填空,下同)
(2)根据表中的规律猜想:用n的代数式表示和S的公式为:S=2+4+6+8+…+2n=n(n+1);
(3)计算:34+36+38+…+108的值.
| 加数的个数n | 和S |
| 1 | 2=1×2 |
| 2 | 2+4=6=2×3 |
| 3 | 2+4+6=12=3×4 |
| 4 | 2+4+6+8=20=4×5 |
| 5 | 2+4+6+8+10=30=5×6 |
(2)根据表中的规律猜想:用n的代数式表示和S的公式为:S=2+4+6+8+…+2n=n(n+1);
(3)计算:34+36+38+…+108的值.
19.已知函数y=x2+3x+c向右平移3个单位后过原点,那么c的值为( )
| A. | 0 | B. | -18 | C. | 3 | D. | -3 |
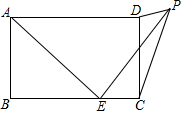 如图,在矩形ABCD中,AB=3,BC=5,点E为BC边上一个动点,连接AE,将线段AE绕点E顺时针旋转90°,点A落在点P处,当点P在矩形ABCD外部时,连接PC、PD.若△DPC为直角三角形,则BE的长为3或$\frac{5+\sqrt{17}}{2}$.
如图,在矩形ABCD中,AB=3,BC=5,点E为BC边上一个动点,连接AE,将线段AE绕点E顺时针旋转90°,点A落在点P处,当点P在矩形ABCD外部时,连接PC、PD.若△DPC为直角三角形,则BE的长为3或$\frac{5+\sqrt{17}}{2}$.