题目内容
2．若a、b、c是三角形的三边长，且满足（a+b）2-（a+c）2=0，则此三角形是（ ）| A． | 等腰三角形 | B． | 等边三角形 | C． | 直角三角形 | D． | 不能确定 |
分析 首先利用平方差公式因式分解，进一步得出三角形边的关系，判定三角形的形状即可．
解答 解：∵（a+b）2-（a+c）2=0，
∴（a+b+a+c）（a+b-a-c）=0，
即（2a+b+c）（b-c）=0，
∵a、b、c是三角形的三边长，
∴b-c=0，b=c，
∴此三角形是等腰三角形．
故选：A．
点评 此题考查因式分解的实际运用，掌握平方差公式是解决问题的关键．
练习册系列答案
阅读快车系列答案
相关题目
12．
如图，在?ABCD中，点E、F分别为AB、AD中点，则图中和△ABF面积相等的三角形有（ ）个．
如图，在?ABCD中，点E、F分别为AB、AD中点，则图中和△ABF面积相等的三角形有（ ）个．| A． | 2个 | B． | 3个 | C． | 4个 | D． | 5个 |
17．科书补助的部分情况：
求获得免费提供教科书补助的七年级的学生人数．
| 年级 项目 | 七 | 八 | 九 | 合计 |
| 每人免费补助金额/元 | 109 | 94 | 47.5 | |
| 人数/人 | 40 | 120 | ||
| 免费补助金额/元 | 1900 | 10095 |
14．若方程（2a+1）x2+bx+c=0是关于x的一元一次方程，则字母系数a，b，c的值必须满足（ ）
| A． | a=-$\frac{1}{2}$，b≠0，c为任何数 | B． | a≠$\frac{1}{2}$，b≠0，c=0 | ||
| C． | a=-$\frac{1}{2}$，b≠0，c≠0 | D． | a=$\frac{1}{2}$，b=0，c为任何数 |
3．
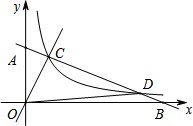如图，在平面直角坐标系中，直线AB与双曲线$y=\frac{2}{x}$相交于C、D两点，已知直线OC解析式为y=2x，S△AOD=6，则D点的坐标为（ ）
如图，在平面直角坐标系中，直线AB与双曲线$y=\frac{2}{x}$相交于C、D两点，已知直线OC解析式为y=2x，S△AOD=6，则D点的坐标为（ ）| A． | $（3，\frac{2}{3}）$ | B． | $（4，\frac{1}{2}）$ | C． | $（5，\frac{2}{5}）$ | D． | $（6，\frac{1}{3}）$ |