题目内容
20. 星期天,小强来到某大型游乐场,想用学过的知识测量摩天轮的高度.如图,在A处测得摩天轮顶端C的仰角为30°,向摩天轮方向走了66米到达B处,此时测得摩天轮顶端C的仰角为45°.请你根据上面的数据计算出摩天轮的高度.(结果精确到0.01米,小强身高忽略不计)
星期天,小强来到某大型游乐场,想用学过的知识测量摩天轮的高度.如图,在A处测得摩天轮顶端C的仰角为30°,向摩天轮方向走了66米到达B处,此时测得摩天轮顶端C的仰角为45°.请你根据上面的数据计算出摩天轮的高度.(结果精确到0.01米,小强身高忽略不计)
分析 过点C作CD⊥AB于点D,在Rt△ACD中,根据三角函数可求CD的长,从而求解.
解答  解:过点C作CD⊥AB于点D,由题意可知∠A=30°,∠CBD=45°.
解:过点C作CD⊥AB于点D,由题意可知∠A=30°,∠CBD=45°.
设CD=x米,则BD=x米,AD=(x+66)米.
在Rt△ACD中,tan∠A=$\frac{CD}{AD}$,即$\frac{x}{x+66}$=tan30°,
解得x=33(1+$\sqrt{3}$)≈90.16.
即摩天轮的高度约为90.16米.
点评 考查了解直角三角形的应用-仰角俯角问题,此题的两个直角三角形拥有公共直角边,能够合理的运用这条公共边是解答此题的关键.

练习册系列答案
相关题目
9.下列方程中,是二元一次方程的是( )
| A. | x+$\frac{1}{y}$=0 | B. | x-y2=3 | C. | x2-2x+1=0 | D. | 3x-5=2y |
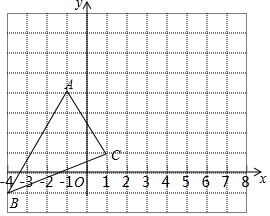 如图,△ABC在直角坐标系中,若把△ABC向右平移5个单位再向上平移3个单位,得到△A1B1C1.
如图,△ABC在直角坐标系中,若把△ABC向右平移5个单位再向上平移3个单位,得到△A1B1C1. 如图,点O是直线AB上一点,∠AOC=$\frac{1}{5}$∠BOC,OC平分∠AOD,求∠BOD的度数.
如图,点O是直线AB上一点,∠AOC=$\frac{1}{5}$∠BOC,OC平分∠AOD,求∠BOD的度数.