题目内容
已知圆内一点P到圆上各点的距离中最短距离为2cm，最长距离为8cm，则过P点的最短弦长为 ．
考点：点与圆的位置关系
专题：
分析：过点P最长的弦就是过点P的直径，过点P最短的弦就是过P点与OP垂直的弦，利用勾股定理可以求出最短的弦．
解答：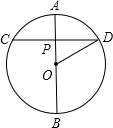
解：如图，AB是过点P最长的弦，是圆的一条直径，
所以AB=10cm．CD是过点P最短的弦，CD⊥OP，
在Rt△OPD中，PD2=OD2-OP2=25-9=16cm，
∴PD=4cm，
∴CD=8cm．
故答案是：8cm．
解：如图，AB是过点P最长的弦，是圆的一条直径，所以AB=10cm．CD是过点P最短的弦，CD⊥OP，
在Rt△OPD中，PD2=OD2-OP2=25-9=16cm，
∴PD=4cm，
∴CD=8cm．
故答案是：8cm．
点评：本题考查了点与圆的位置关系的判断．关键要记住若半径为r，点到圆心的距离为d，则有：当d＞r时，点在圆外；当d=r时，点在圆上，当d＜r时，点在圆内．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
如图所示，菱形ABCD中，对角线AC、BC相交于点O，H为AD边中点，菱形ABCD的周长为16，则OH的长等于（ ）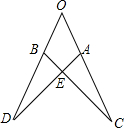
如图，若△OAD≌△OBC，且∠O=50°，∠D=35°，则∠AEC=
作图题：