题目内容
 如图,四边形ABCD与四边形A′B′C′D′全等,则∠A′=
如图,四边形ABCD与四边形A′B′C′D′全等,则∠A′=(1)已知△ABC≌△DEF,∠A=∠D,∠C=∠F,∠B=45°,EF=6cm,则∠E=
(2)已知△ABC≌△A′B′C′,△A′B′C′的周长为32cm,A′B′=9cm,B′C′=12cm,则AC=
考点:全等三角形的性质
专题:
分析:根据全等图形定义可得:∠A′=∠D,∠A=∠D′,B′C′=BC,AD=A′D′;
(1)根据全等三角形,对应边相等、对应角相等可得∠E=∠B=45°,BC=EF=6cm;
(2)根据已知条件求出A′C′长,再根据全等三角形,对应边相等可得答案.
(1)根据全等三角形,对应边相等、对应角相等可得∠E=∠B=45°,BC=EF=6cm;
(2)根据已知条件求出A′C′长,再根据全等三角形,对应边相等可得答案.
解答:解:∵四边形ABCD与四边形A′B′C′D′全等,
∴∠A′=120°,∠A=70°,B′C′=BC=12,AD=A′D′=6;
(1)如图:
 ,
,
∵△ABC≌△DEF,
∴∠E=∠B=45°,BC=EF=6cm;
(2)∵△A′B′C′的周长为32cm,A′B′=9cm,B′C′=12cm,
∴A′C′=32-9-12=11cm,
∵△ABC≌△A′B′C′,
∴AC=A′C′=11cm.
∴∠A′=120°,∠A=70°,B′C′=BC=12,AD=A′D′=6;
(1)如图:
 ,
,∵△ABC≌△DEF,
∴∠E=∠B=45°,BC=EF=6cm;
(2)∵△A′B′C′的周长为32cm,A′B′=9cm,B′C′=12cm,
∴A′C′=32-9-12=11cm,
∵△ABC≌△A′B′C′,
∴AC=A′C′=11cm.
点评:此题主要考查了全等三角形的性质,关键是掌握全等三角形,对应边相等、对应角相等.

练习册系列答案
相关题目
?ABCD的对角线AC、BD相交于O,AC=4,BD=5,BC=3,则△BOC的周长为( )
| A、7.5 | B、12 |
| C、6 | D、无法确定 |
 如图,点A用(3,1)表示,点B用(8,5)表示.若用(3,1)→(3,3)→(5,3)→(5,4)→(8,4)→(8,5)表示由A到B的一种走法,并规定从A到B只能向上或向右走,用上述表示法写出另两种走法,并判断这几种走法的路程是否相等.
如图,点A用(3,1)表示,点B用(8,5)表示.若用(3,1)→(3,3)→(5,3)→(5,4)→(8,4)→(8,5)表示由A到B的一种走法,并规定从A到B只能向上或向右走,用上述表示法写出另两种走法,并判断这几种走法的路程是否相等.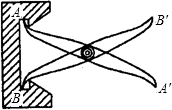 如图,把两根钢条AA′,BB′的中点O连在一起,可以做成一个测量工件内槽宽的工具(工人把这种工具叫卡钳)只要量出A′B′的长度,就可以知道工件的内径AB是否符合标准,你能简要说出工人这样测量的道理吗?
如图,把两根钢条AA′,BB′的中点O连在一起,可以做成一个测量工件内槽宽的工具(工人把这种工具叫卡钳)只要量出A′B′的长度,就可以知道工件的内径AB是否符合标准,你能简要说出工人这样测量的道理吗?