题目内容
18.某同学将一块正方形铁皮剪去四个小正方形,做成一个无盖盒子,如图1所示.(1)若剪下的四个小正方形的边长均为6cm,且无盖盒子的容积为3750cm3,则原正方形的边长为多少?
(2)为了制作一个有盖的盒子,他又设计了如图2的方案,为了使有盖盒子的高于容积和图1中无盖盒子的高与容积一样,则需要边长多大的正方形铁皮?
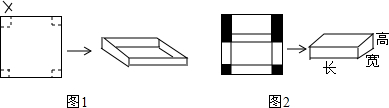
分析 (1)设正方形铁皮的边长应是x厘米,则做成没有盖的长方体盒子的长、宽为(x-6×2)厘米,高为6厘米,根据长方体的体积计算公式列方程解答即可;
(2)设需要边长为a厘米的正方形铁皮,有盖盒子长为(a-6×2)厘米,宽为$\frac{1}{2}$(a-6×2)厘米,高为6厘米,根据长方体的体积计算公式列方程解答即可.
解答 解:(1)设原正方形铁皮的边长应是x厘米,则没有盖的长方体盒子的长、宽为(x-6×2)厘米,高为6厘米,根据题意列方程得,
(x-6×2)(x-6×2)×6=3750,
解得:x1=37,x2=-13(不合题意,舍去).
答:正方形铁皮的边长应是37厘米.
(2)设需要边长为a厘米的正方形铁皮,由题意得
$\frac{1}{2}$(a-6×2)(a-6×2)×6=3750
解得:a1=25$\sqrt{2}$+12,a2=12-25$\sqrt{2}$(不合题意,舍去).
答:正方形铁皮的边长应是25$\sqrt{2}$+12厘米.
点评 本题考查了一元二次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
12. 如图,⊙O中,弧AB=弧AC,∠C=75°,则∠A=( )
如图,⊙O中,弧AB=弧AC,∠C=75°,则∠A=( )
 如图,⊙O中,弧AB=弧AC,∠C=75°,则∠A=( )
如图,⊙O中,弧AB=弧AC,∠C=75°,则∠A=( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
 点A、B、C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点c分别以每秒2个单位长度和5个单位长度的速度向右运动.请问;BC-AB的值是否随运动时间t的变化而改变?若变化,请说明理由;若不变,请求其值.
点A、B、C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点c分别以每秒2个单位长度和5个单位长度的速度向右运动.请问;BC-AB的值是否随运动时间t的变化而改变?若变化,请说明理由;若不变,请求其值.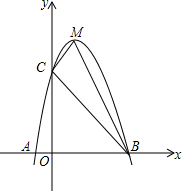 如图,二次函数y=ax2+bx+c的图象交x轴于A(x1,0),B(x2,0)(x1<x2),交y轴于点C(0,3),其顶点M(1,4).
如图,二次函数y=ax2+bx+c的图象交x轴于A(x1,0),B(x2,0)(x1<x2),交y轴于点C(0,3),其顶点M(1,4).